Strategic Resource Selection with Homophilic Agents
Paper and Code
May 01, 2023
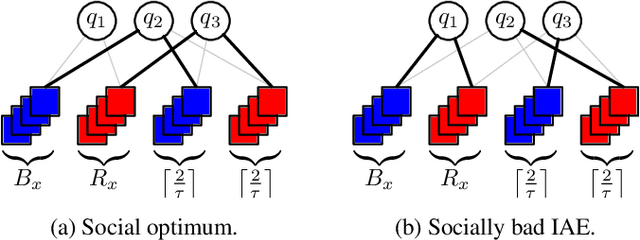
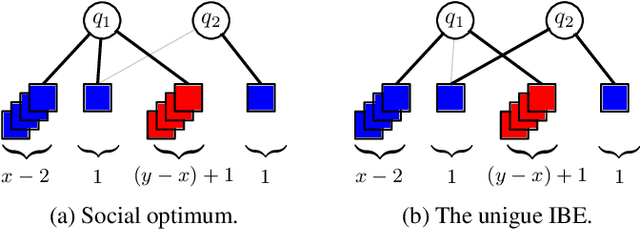
The strategic selection of resources by selfish agents is a classic research direction, with Resource Selection Games and Congestion Games as prominent examples. In these games, agents select available resources and their utility then depends on the number of agents using the same resources. This implies that there is no distinction between the agents, i.e., they are anonymous. We depart from this very general setting by proposing Resource Selection Games with heterogeneous agents that strive for joint resource usage with similar agents. So, instead of the number of other users of a given resource, our model considers agents with different types and the decisive feature is the fraction of same-type agents among the users. More precisely, similarly to Schelling Games, there is a tolerance threshold $\tau \in [0,1]$ which specifies the agents' desired minimum fraction of same-type agents on a resource. Agents strive to select resources where at least a $\tau$-fraction of those resources' users have the same type as themselves. For $\tau=1$, our model generalizes Hedonic Diversity Games with a peak at $1$. For our general model, we consider the existence and quality of equilibria and the complexity of maximizing social welfare. Additionally, we consider a bounded rationality model, where agents can only estimate the utility of a resource, since they only know the fraction of same-type agents on a given resource, but not the exact numbers. Thus, they cannot know the impact a strategy change would have on a target resource. Interestingly, we show that this type of bounded rationality yields favorable game-theoretic properties and specific equilibria closely approximate equilibria of the full knowledge setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge