Run Time Bounds for Integer-Valued OneMax Functions
Paper and Code
Jul 21, 2023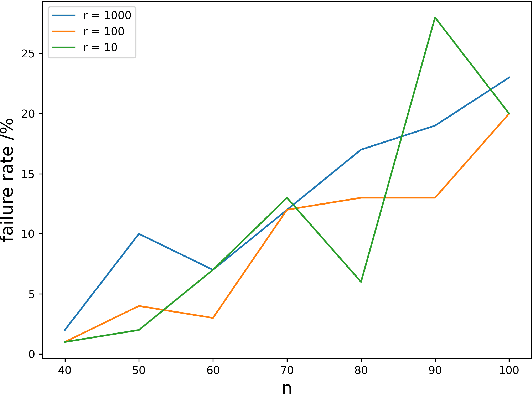
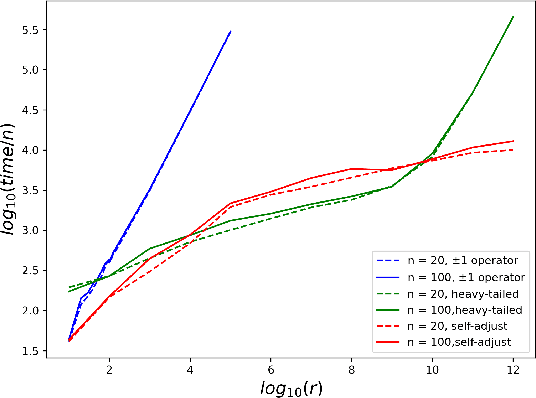
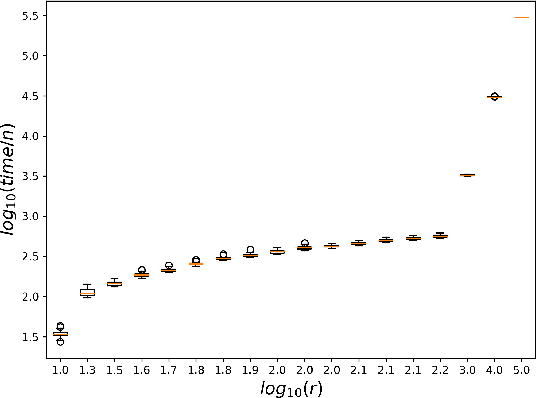
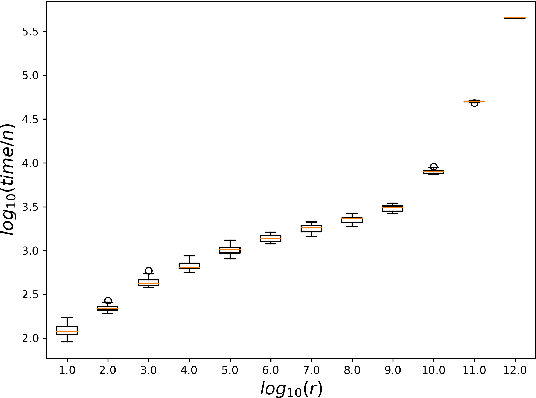
While most theoretical run time analyses of discrete randomized search heuristics focused on finite search spaces, we consider the search space $\mathbb{Z}^n$. This is a further generalization of the search space of multi-valued decision variables $\{0,\ldots,r-1\}^n$. We consider as fitness functions the distance to the (unique) non-zero optimum $a$ (based on the $L_1$-metric) and the \ooea which mutates by applying a step-operator on each component that is determined to be varied. For changing by $\pm 1$, we show that the expected optimization time is $\Theta(n \cdot (|a|_{\infty} + \log(|a|_H)))$. In particular, the time is linear in the maximum value of the optimum $a$. Employing a different step operator which chooses a step size from a distribution so heavy-tailed that the expectation is infinite, we get an optimization time of $O(n \cdot \log^2 (|a|_1) \cdot \left(\log (\log (|a|_1))\right)^{1 + \epsilon})$. Furthermore, we show that RLS with step size adaptation achieves an optimization time of $\Theta(n \cdot \log(|a|_1))$. We conclude with an empirical analysis, comparing the above algorithms also with a variant of CMA-ES for discrete search spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge