(1+1) Genetic Programming With Functionally Complete Instruction Sets Can Evolve Boolean Conjunctions and Disjunctions with Arbitrarily Small Error

Recently it has been proven that simple GP systems can efficiently evolve a conjunction of $n$ variables if they are equipped with the minimal required components. In this paper, we make a considerable step forward by analysing the behaviour and performance of a GP system for evolving a Boolean conjunction or disjunction of $n$ variables using a complete function set that allows the expression of any Boolean function of up to $n$ variables. First we rigorously prove that a GP system using the complete truth table to evaluate the program quality, and equipped with both the AND and OR operators and positive literals, evolves the exact target function in $O(\ell n \log^2 n)$ iterations in expectation, where $\ell \geq n$ is a limit on the size of any accepted tree. Additionally, we show that when a polynomial sample of possible inputs is used to evaluate the solution quality, conjunctions or disjunctions with any polynomially small generalisation error can be evolved with probability $1 - O(\log^2(n)/n)$. The latter result also holds if GP uses AND, OR and positive and negated literals, thus has the power to express any Boolean function of $n$ distinct variables. To prove our results we introduce a super-multiplicative drift theorem that gives significantly stronger runtime bounds when the expected progress is only slightly super-linear in the distance from the optimum.

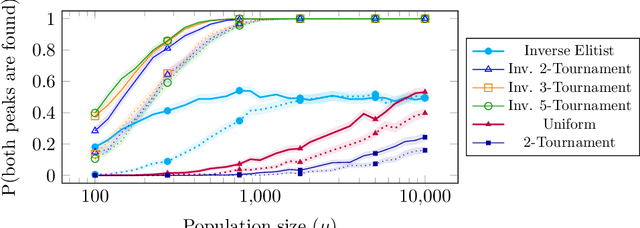
On Steady-State Evolutionary Algorithms and Selective Pressure: Why Inverse Rank-Based Allocation of Reproductive Trials is Best

We analyse the impact of the selective pressure for the global optimisation capabilities of steady-state EAs. For the standard bimodal benchmark function \twomax we rigorously prove that using uniform parent selection leads to exponential runtimes with high probability to locate both optima for the standard ($\mu$+1)~EA and ($\mu$+1)~RLS with any polynomial population sizes. On the other hand, we prove that selecting the worst individual as parent leads to efficient global optimisation with overwhelming probability for reasonable population sizes. Since always selecting the worst individual may have detrimental effects for escaping from local optima, we consider the performance of stochastic parent selection operators with low selective pressure for a function class called \textsc{TruncatedTwoMax} where one slope is shorter than the other. An experimental analysis shows that the EAs equipped with inverse tournament selection, where the loser is selected for reproduction and small tournament sizes, globally optimise \textsc{TwoMax} efficiently and effectively escape from local optima of \textsc{TruncatedTwoMax} with high probability. Thus they identify both optima efficiently while uniform (or stronger) selection fails in theory and in practice. We then show the power of inverse selection on function classes from the literature where populations are essential by providing rigorous proofs or experimental evidence that it outperforms uniform selection equipped with or without a restart strategy. We conclude the paper by confirming our theoretical insights with an empirical analysis of the different selective pressures on standard benchmarks of the classical MaxSat and Multidimensional Knapsack Problems.

On the Impact of the Cutoff Time on the Performance of Algorithm Configurators

Algorithm configurators are automated methods to optimise the parameters of an algorithm for a class of problems. We evaluate the performance of a simple random local search configurator (ParamRLS) for tuning the neighbourhood size $k$ of the RLS$_k$ algorithm. We measure performance as the expected number of configuration evaluations required to identify the optimal value for the parameter. We analyse the impact of the cutoff time $\kappa$ (the time spent evaluating a configuration for a problem instance) on the expected number of configuration evaluations required to find the optimal parameter value, where we compare configurations using either best found fitness values (ParamRLS-F) or optimisation times (ParamRLS-T). We consider tuning RLS$_k$ for a variant of the Ridge function class (Ridge*), where the performance of each parameter value does not change during the run, and for the OneMax function class, where longer runs favour smaller $k$. We rigorously prove that ParamRLS-F efficiently tunes RLS$_k$ for Ridge* for any $\kappa$ while ParamRLS-T requires at least quadratic $\kappa$. For OneMax ParamRLS-F identifies $k=1$ as optimal with linear $\kappa$ while ParamRLS-T requires a $\kappa$ of at least $\Omega(n\log n)$. For smaller $\kappa$ ParamRLS-F identifies that $k>1$ performs better while ParamRLS-T returns $k$ chosen uniformly at random.

Evolving Boolean Functions with Conjunctions and Disjunctions via Genetic Programming

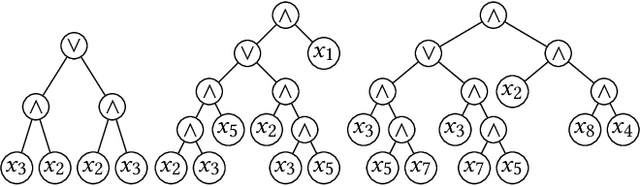
Recently it has been proved that simple GP systems can efficiently evolve the conjunction of $n$ variables if they are equipped with the minimal required components. In this paper, we make a considerable step forward by analysing the behaviour and performance of the GP system for evolving a Boolean function with unknown components, i.e., the function may consist of both conjunctions and disjunctions. We rigorously prove that if the target function is the conjunction of $n$ variables, then the RLS-GP using the complete truth table to evaluate program quality evolves the exact target function in $O(\ell n \log^2 n)$ iterations in expectation, where $\ell \geq n$ is a limit on the size of any accepted tree. When, as in realistic applications, only a polynomial sample of possible inputs is used to evaluate solution quality, we show how RLS-GP can evolve a conjunction with any polynomially small generalisation error with probability $1 - O(\log^2(n)/n)$. To produce our results we introduce a super-multiplicative drift theorem that gives significantly stronger runtime bounds when the expected progress is only slightly super-linear in the distance from the optimum.

On Inversely Proportional Hypermutations with Mutation Potential

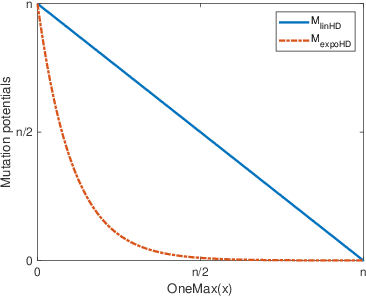
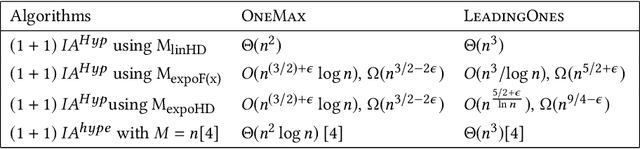
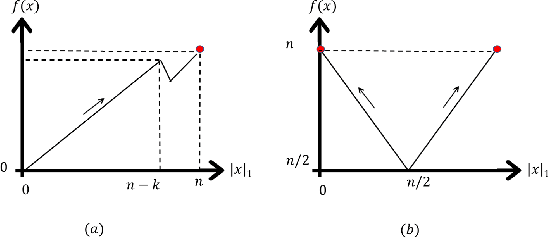
Artificial Immune Systems (AIS) employing hypermutations with linear static mutation potential have recently been shown to be very effective at escaping local optima of combinatorial optimisation problems at the expense of being slower during the exploitation phase compared to standard evolutionary algorithms. In this paper we prove that considerable speed-ups in the exploitation phase may be achieved with dynamic inversely proportional mutation potentials (IPM) and argue that the potential should decrease inversely to the distance to the optimum rather than to the difference in fitness. Afterwards we define a simple (1+1)~Opt-IA, that uses IPM hypermutations and ageing, for realistic applications where optimal solutions are unknown. The aim of the AIS is to approximate the ideal behaviour of the inversely proportional hypermutations better and better as the search space is explored. We prove that such desired behaviour, and related speed-ups, occur for a well-studied bimodal benchmark function called \textsc{TwoMax}. Furthermore, we prove that the (1+1)~Opt-IA with IPM efficiently optimises a third bimodal function, \textsc{Cliff}, by escaping its local optima while Opt-IA with static potential cannot, thus requires exponential expected runtime in the distance between the cliff and the optimum.

On the Benefits of Populations on the Exploitation Speed of Standard Steady-State Genetic Algorithms

It is generally accepted that populations are useful for the global exploration of multi-modal optimisation problems. Indeed, several theoretical results are available showing such advantages over single-trajectory search heuristics. In this paper we provide evidence that evolving populations via crossover and mutation may also benefit the optimisation time for hillclimbing unimodal functions. In particular, we prove bounds on the expected runtime of the standard ($\mu$+1)~GA for OneMax that are lower than its unary black box complexity and decrease in the leading constant with the population size up to $\mu=O(\sqrt{\log n})$. Our analysis suggests that the optimal mutation strategy is to flip two bits most of the time. To achieve the results we provide two interesting contributions to the theory of randomised search heuristics: 1) A novel application of drift analysis which compares absorption times of different Markov chains without defining an explicit potential function. 2) The inversion of fundamental matrices to calculate the absorption times of the Markov chains. The latter strategy was previously proposed in the literature but to the best of our knowledge this is the first time is has been used to show non-trivial bounds on expected runtimes.

Computational Complexity Analysis of Genetic Programming

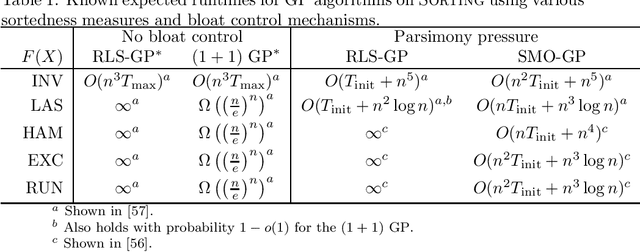
Genetic Programming (GP) is an evolutionary computation technique to solve problems in an automated, domain-independent way. Rather than identifying the optimum of a function as in more traditional evolutionary optimization, the aim of GP is to evolve computer programs with a given functionality. A population of programs is evolved using variation operators inspired by Darwinian evolution (crossover and mutation) and natural selection principles to guide the search process towards better programs. While many GP applications have produced human competitive results, the theoretical understanding of what problem characteristics and algorithm properties allow GP to be effective is comparatively limited. Compared to traditional evolutionary algorithms for function optimization, GP applications are further complicated by two additional factors: the variable length representation of candidate programs, and the difficulty of evaluating their quality efficiently. Such difficulties considerably impact the runtime analysis of GP where space complexity also comes into play. As a result initial complexity analyses of GP focused on restricted settings such as evolving trees with given structures or estimating the quality of solutions using only a small polynomial number of input/output examples. However, the first runtime analyses concerning GP applications for evolving proper functions with defined input/output behavior have recently appeared. In this chapter, we present an overview of the state-of-the-art.

Artificial Immune Systems Can Find Arbitrarily Good Approximations for the NP-Hard Partition Problem

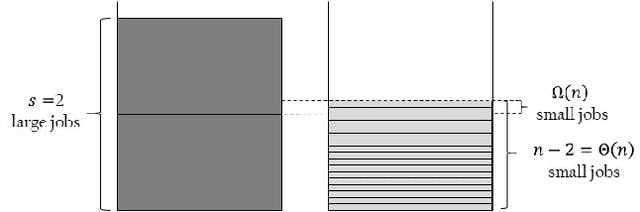
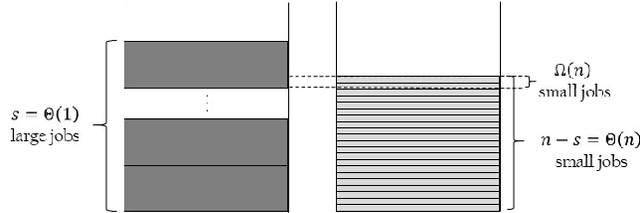
Typical Artificial Immune System (AIS) operators such as hypermutations with mutation potential and ageing allow to efficiently overcome local optima from which Evolutionary Algorithms (EAs) struggle to escape. Such behaviour has been shown for artificial example functions such as Jump, Cliff or Trap constructed especially to show difficulties that EAs may encounter during the optimisation process. However, no evidence is available indicating that similar effects may also occur in more realistic problems. In this paper we perform an analysis for the standard NP-Hard \partition problem from combinatorial optimisation and rigorously show that hypermutations and ageing allow AISs to efficiently escape from local optima where standard EAs require exponential time. As a result we prove that while EAs and Random Local Search may get trapped on 4/3 approximations, AISs find arbitrarily good approximate solutions of ratio (1+$\epsilon$) for any constant $\epsilon$ within a time that is polynomial in the problem size and exponential only in $1/\epsilon$.

Fast Artificial Immune Systems

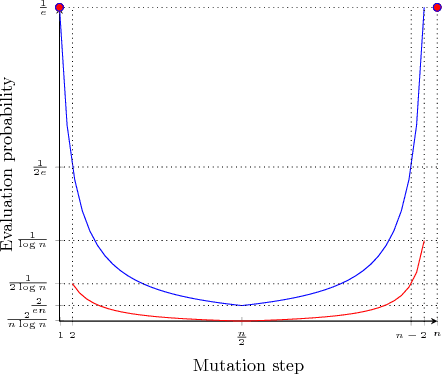
Various studies have shown that characteristic Artificial Immune System (AIS) operators such as hypermutations and ageing can be very efficient at escaping local optima of multimodal optimisation problems. However, this efficiency comes at the expense of considerably slower runtimes during the exploitation phase compared to standard evolutionary algorithms. We propose modifications to the traditional `hypermutations with mutation potential' (HMP) that allow them to be efficient at exploitation as well as maintaining their effective explorative characteristics. Rather than deterministically evaluating fitness after each bitflip of a hypermutation, we sample the fitness function stochastically with a `parabolic' distribution which allows the `stop at first constructive mutation' (FCM) variant of HMP to reduce the linear amount of wasted function evaluations when no improvement is found to a constant. By returning the best sampled solution during the hypermutation, rather than the first constructive mutation, we then turn the extremely inefficient HMP operator without FCM, into a very effective operator for the standard Opt-IA AIS using hypermutation, cloning and ageing. We rigorously prove the effectiveness of the two proposed operators by analysing them on all problems where the performance of HPM is rigorously understood in the literature. %

When Hypermutations and Ageing Enable Artificial Immune Systems to Outperform Evolutionary Algorithms

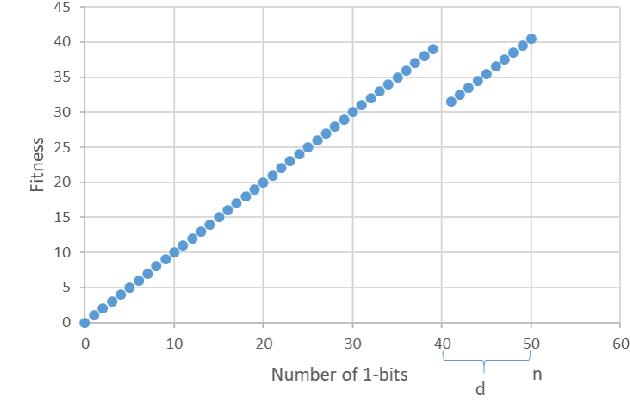
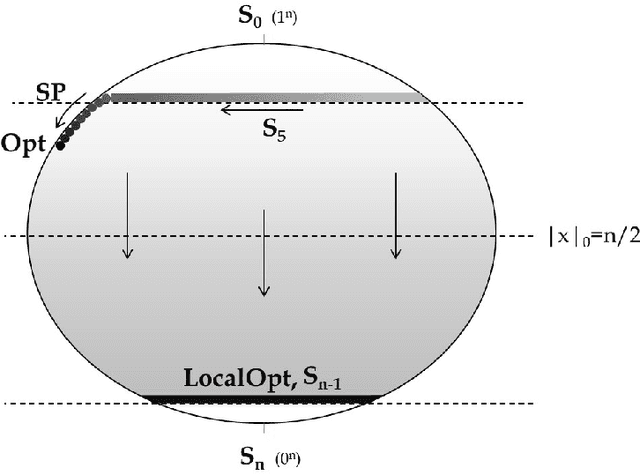
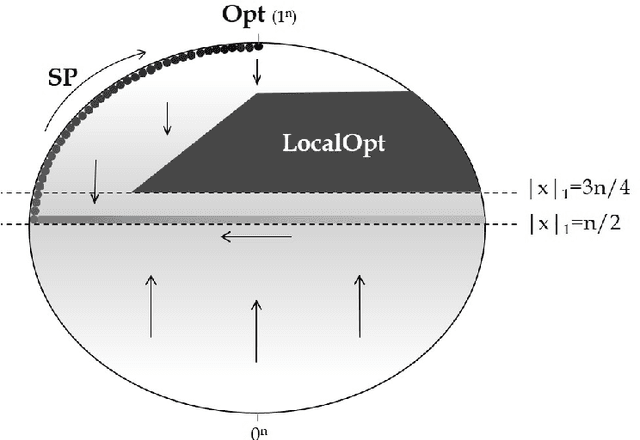
We present a time complexity analysis of the Opt-IA artificial immune system (AIS). We first highlight the power and limitations of its distinguishing operators (i.e., hypermutations with mutation potential and ageing) by analysing them in isolation. Recent work has shown that ageing combined with local mutations can help escape local optima on a dynamic optimisation benchmark function. We generalise this result by rigorously proving that, compared to evolutionary algorithms (EAs), ageing leads to impressive speed-ups on the standard Cliff benchmark function both when using local and global mutations. Unless the stop at first constructive mutation (FCM) mechanism is applied, we show that hypermutations require exponential expected runtime to optimise any function with a polynomial number of optima. If instead FCM is used, the expected runtime is at most a linear factor larger than the upper bound achieved for any random local search algorithm using the artificial fitness levels method. Nevertheless, we prove that algorithms using hypermutations can be considerably faster than EAs at escaping local optima. An analysis of the complete Opt-IA reveals that it is efficient on the previously considered functions and highlights problems where the use of the full algorithm is crucial. We complete the picture by presenting a class of functions for which Opt-IA fails with overwhelming probability while standard EAs are efficient.