On Steady-State Evolutionary Algorithms and Selective Pressure: Why Inverse Rank-Based Allocation of Reproductive Trials is Best
Paper and Code
Mar 18, 2021


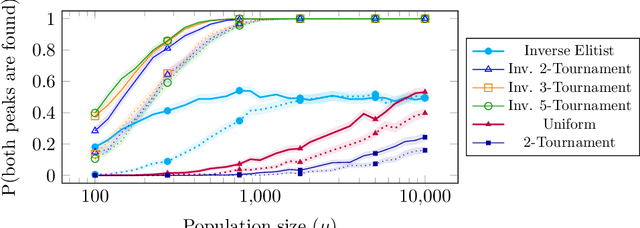
We analyse the impact of the selective pressure for the global optimisation capabilities of steady-state EAs. For the standard bimodal benchmark function \twomax we rigorously prove that using uniform parent selection leads to exponential runtimes with high probability to locate both optima for the standard ($\mu$+1)~EA and ($\mu$+1)~RLS with any polynomial population sizes. On the other hand, we prove that selecting the worst individual as parent leads to efficient global optimisation with overwhelming probability for reasonable population sizes. Since always selecting the worst individual may have detrimental effects for escaping from local optima, we consider the performance of stochastic parent selection operators with low selective pressure for a function class called \textsc{TruncatedTwoMax} where one slope is shorter than the other. An experimental analysis shows that the EAs equipped with inverse tournament selection, where the loser is selected for reproduction and small tournament sizes, globally optimise \textsc{TwoMax} efficiently and effectively escape from local optima of \textsc{TruncatedTwoMax} with high probability. Thus they identify both optima efficiently while uniform (or stronger) selection fails in theory and in practice. We then show the power of inverse selection on function classes from the literature where populations are essential by providing rigorous proofs or experimental evidence that it outperforms uniform selection equipped with or without a restart strategy. We conclude the paper by confirming our theoretical insights with an empirical analysis of the different selective pressures on standard benchmarks of the classical MaxSat and Multidimensional Knapsack Problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge