(1+1) Genetic Programming With Functionally Complete Instruction Sets Can Evolve Boolean Conjunctions and Disjunctions with Arbitrarily Small Error

Recently it has been proven that simple GP systems can efficiently evolve a conjunction of $n$ variables if they are equipped with the minimal required components. In this paper, we make a considerable step forward by analysing the behaviour and performance of a GP system for evolving a Boolean conjunction or disjunction of $n$ variables using a complete function set that allows the expression of any Boolean function of up to $n$ variables. First we rigorously prove that a GP system using the complete truth table to evaluate the program quality, and equipped with both the AND and OR operators and positive literals, evolves the exact target function in $O(\ell n \log^2 n)$ iterations in expectation, where $\ell \geq n$ is a limit on the size of any accepted tree. Additionally, we show that when a polynomial sample of possible inputs is used to evaluate the solution quality, conjunctions or disjunctions with any polynomially small generalisation error can be evolved with probability $1 - O(\log^2(n)/n)$. The latter result also holds if GP uses AND, OR and positive and negated literals, thus has the power to express any Boolean function of $n$ distinct variables. To prove our results we introduce a super-multiplicative drift theorem that gives significantly stronger runtime bounds when the expected progress is only slightly super-linear in the distance from the optimum.

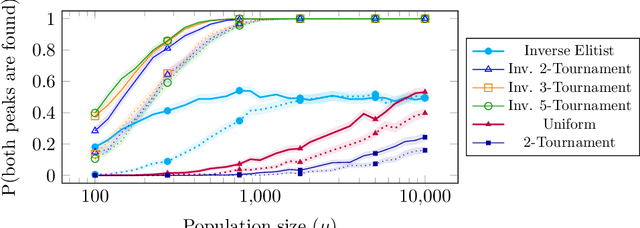
On Steady-State Evolutionary Algorithms and Selective Pressure: Why Inverse Rank-Based Allocation of Reproductive Trials is Best

We analyse the impact of the selective pressure for the global optimisation capabilities of steady-state EAs. For the standard bimodal benchmark function \twomax we rigorously prove that using uniform parent selection leads to exponential runtimes with high probability to locate both optima for the standard ($\mu$+1)~EA and ($\mu$+1)~RLS with any polynomial population sizes. On the other hand, we prove that selecting the worst individual as parent leads to efficient global optimisation with overwhelming probability for reasonable population sizes. Since always selecting the worst individual may have detrimental effects for escaping from local optima, we consider the performance of stochastic parent selection operators with low selective pressure for a function class called \textsc{TruncatedTwoMax} where one slope is shorter than the other. An experimental analysis shows that the EAs equipped with inverse tournament selection, where the loser is selected for reproduction and small tournament sizes, globally optimise \textsc{TwoMax} efficiently and effectively escape from local optima of \textsc{TruncatedTwoMax} with high probability. Thus they identify both optima efficiently while uniform (or stronger) selection fails in theory and in practice. We then show the power of inverse selection on function classes from the literature where populations are essential by providing rigorous proofs or experimental evidence that it outperforms uniform selection equipped with or without a restart strategy. We conclude the paper by confirming our theoretical insights with an empirical analysis of the different selective pressures on standard benchmarks of the classical MaxSat and Multidimensional Knapsack Problems.

Evolving Boolean Functions with Conjunctions and Disjunctions via Genetic Programming

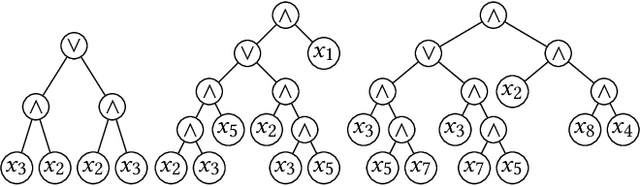
Recently it has been proved that simple GP systems can efficiently evolve the conjunction of $n$ variables if they are equipped with the minimal required components. In this paper, we make a considerable step forward by analysing the behaviour and performance of the GP system for evolving a Boolean function with unknown components, i.e., the function may consist of both conjunctions and disjunctions. We rigorously prove that if the target function is the conjunction of $n$ variables, then the RLS-GP using the complete truth table to evaluate program quality evolves the exact target function in $O(\ell n \log^2 n)$ iterations in expectation, where $\ell \geq n$ is a limit on the size of any accepted tree. When, as in realistic applications, only a polynomial sample of possible inputs is used to evaluate solution quality, we show how RLS-GP can evolve a conjunction with any polynomially small generalisation error with probability $1 - O(\log^2(n)/n)$. To produce our results we introduce a super-multiplicative drift theorem that gives significantly stronger runtime bounds when the expected progress is only slightly super-linear in the distance from the optimum.

Computational Complexity Analysis of Genetic Programming

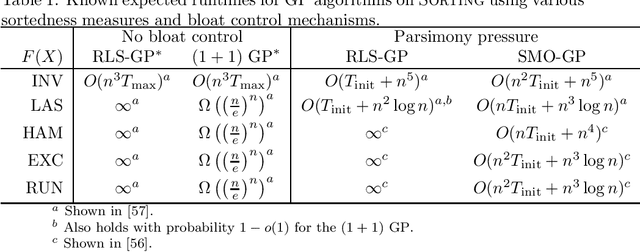
Genetic Programming (GP) is an evolutionary computation technique to solve problems in an automated, domain-independent way. Rather than identifying the optimum of a function as in more traditional evolutionary optimization, the aim of GP is to evolve computer programs with a given functionality. A population of programs is evolved using variation operators inspired by Darwinian evolution (crossover and mutation) and natural selection principles to guide the search process towards better programs. While many GP applications have produced human competitive results, the theoretical understanding of what problem characteristics and algorithm properties allow GP to be effective is comparatively limited. Compared to traditional evolutionary algorithms for function optimization, GP applications are further complicated by two additional factors: the variable length representation of candidate programs, and the difficulty of evaluating their quality efficiently. Such difficulties considerably impact the runtime analysis of GP where space complexity also comes into play. As a result initial complexity analyses of GP focused on restricted settings such as evolving trees with given structures or estimating the quality of solutions using only a small polynomial number of input/output examples. However, the first runtime analyses concerning GP applications for evolving proper functions with defined input/output behavior have recently appeared. In this chapter, we present an overview of the state-of-the-art.

Hyper-heuristics Can Achieve Optimal Performance for Pseudo-Boolean Optimisation

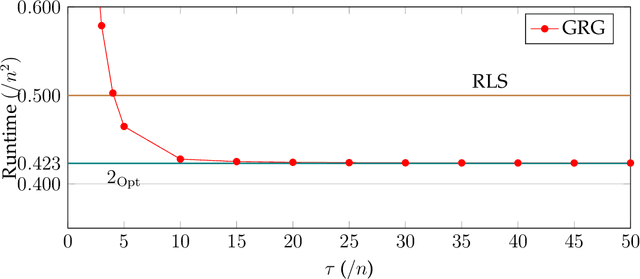
Selection hyper-heuristics are randomised search methodologies which choose and execute heuristics from a set of low-level heuristics. Recent research for the LeadingOnes benchmark function has shown that the standard Simple Random, Permutation, Random Gradient, Greedy and Reinforcement Learning selection mechanisms show no effects of learning. The idea behind the learning mechanisms is to continue to exploit the currently selected heuristic as long as it is successful. However, the probability that a promising heuristic is successful in the next step is relatively low when perturbing a reasonable solution to a combinatorial optimisation problem. In this paper we generalise the `simple' selection-perturbation mechanisms so success can be measured over some fixed period of time tau, rather than in a single iteration. We present a benchmark function where it is necessary to learn to exploit a particular low-level heuristic, rigorously proving that it makes the difference between an efficient and an inefficient algorithm. For LeadingOnes we prove that the Generalised Random Gradient, and the Generalised Greedy Gradient hyper-heuristics achieve optimal performance, while Generalised Greedy, although not as fast, still outperforms Random Local Search. The performance of the former two hyper-heuristics improves as the number of operators to choose from increases, while that of the Generalised Greedy hyper-heuristic does not. Experimental analyses confirm these results for realistic problem sizes and shed some light on the best choices of the parameter tau in various situations.