Hyper-heuristics Can Achieve Optimal Performance for Pseudo-Boolean Optimisation
Paper and Code
Jan 23, 2018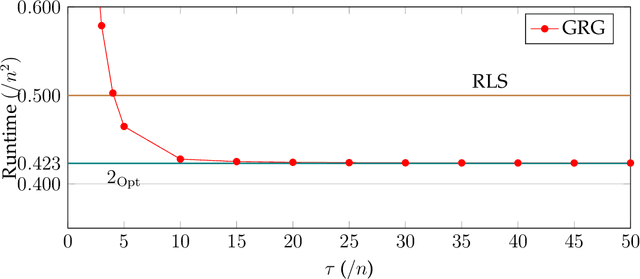



Selection hyper-heuristics are randomised search methodologies which choose and execute heuristics from a set of low-level heuristics. Recent research for the LeadingOnes benchmark function has shown that the standard Simple Random, Permutation, Random Gradient, Greedy and Reinforcement Learning selection mechanisms show no effects of learning. The idea behind the learning mechanisms is to continue to exploit the currently selected heuristic as long as it is successful. However, the probability that a promising heuristic is successful in the next step is relatively low when perturbing a reasonable solution to a combinatorial optimisation problem. In this paper we generalise the `simple' selection-perturbation mechanisms so success can be measured over some fixed period of time tau, rather than in a single iteration. We present a benchmark function where it is necessary to learn to exploit a particular low-level heuristic, rigorously proving that it makes the difference between an efficient and an inefficient algorithm. For LeadingOnes we prove that the Generalised Random Gradient, and the Generalised Greedy Gradient hyper-heuristics achieve optimal performance, while Generalised Greedy, although not as fast, still outperforms Random Local Search. The performance of the former two hyper-heuristics improves as the number of operators to choose from increases, while that of the Generalised Greedy hyper-heuristic does not. Experimental analyses confirm these results for realistic problem sizes and shed some light on the best choices of the parameter tau in various situations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge