A Runtime Analysis of the Multi-Valued Compact Genetic Algorithm on Generalized LeadingOnes

In the literature on runtime analyses of estimation of distribution algorithms (EDAs), researchers have recently explored univariate EDAs for multi-valued decision variables. Particularly, Jedidia et al. gave the first runtime analysis of the multi-valued UMDA on the r-valued LeadingOnes (r-LeadingOnes) functions and Adak et al. gave the first runtime analysis of the multi-valued cGA (r-cGA) on the r-valued OneMax function. We utilize their framework to conduct an analysis of the multi-valued cGA on the r-valued LeadingOnes function. Even for the binary case, a runtime analysis of the classical cGA on LeadingOnes was not yet available. In this work, we show that the runtime of the r-cGA on r-LeadingOnes is O(n^2r^2 log^3 n log^2 r) with high probability.

Sliding Window 3-Objective Pareto Optimization for Problems with Chance Constraints

Constrained single-objective problems have been frequently tackled by evolutionary multi-objective algorithms where the constraint is relaxed into an additional objective. Recently, it has been shown that Pareto optimization approaches using bi-objective models can be significantly sped up using sliding windows (Neumann and Witt, ECAI 2023). In this paper, we extend the sliding window approach to $3$-objective formulations for tackling chance constrained problems. On the theoretical side, we show that our new sliding window approach improves previous runtime bounds obtained in (Neumann and Witt, GECCO 2023) while maintaining the same approximation guarantees. Our experimental investigations for the chance constrained dominating set problem show that our new sliding window approach allows one to solve much larger instances in a much more efficient way than the 3-objective approach presented in (Neumann and Witt, GECCO 2023).

Runtime Analysis of a Multi-Valued Compact Genetic Algorithm on Generalized OneMax

A class of metaheuristic techniques called estimation-of-distribution algorithms (EDAs) are employed in optimization as more sophisticated substitutes for traditional strategies like evolutionary algorithms. EDAs generally drive the search for the optimum by creating explicit probabilistic models of potential candidate solutions through repeated sampling and selection from the underlying search space. Most theoretical research on EDAs has focused on pseudo-Boolean optimization. Jedidia et al. (GECCO 2023) proposed the first EDAs for optimizing problems involving multi-valued decision variables. By building a framework, they have analyzed the runtime of a multi-valued UMDA on the r-valued LeadingOnes function. Using their framework, here we focus on the multi-valued compact genetic algorithm (r-cGA) and provide a first runtime analysis of a generalized OneMax function. To prove our results, we investigate the effect of genetic drift and progress of the probabilistic model towards the optimum. After finding the right algorithm parameters, we prove that the r-cGA solves this r-valued OneMax problem efficiently. We show that with high probability, the runtime bound is O(r2 n log2 r log3 n). At the end of experiments, we state one conjecture related to the expected runtime of another variant of multi-valued OneMax function.

A Flexible Evolutionary Algorithm With Dynamic Mutation Rate Archive

We propose a new, flexible approach for dynamically maintaining successful mutation rates in evolutionary algorithms using $k$-bit flip mutations. The algorithm adds successful mutation rates to an archive of promising rates that are favored in subsequent steps. Rates expire when their number of unsuccessful trials has exceeded a threshold, while rates currently not present in the archive can enter it in two ways: (i) via user-defined minimum selection probabilities for rates combined with a successful step or (ii) via a stagnation detection mechanism increasing the value for a promising rate after the current bit-flip neighborhood has been explored with high probability. For the minimum selection probabilities, we suggest different options, including heavy-tailed distributions. We conduct rigorous runtime analysis of the flexible evolutionary algorithm on the OneMax and Jump functions, on general unimodal functions, on minimum spanning trees, and on a class of hurdle-like functions with varying hurdle width that benefit particularly from the archive of promising mutation rates. In all cases, the runtime bounds are close to or even outperform the best known results for both stagnation detection and heavy-tailed mutations.

First Steps towards a Runtime Analysis of Neuroevolution

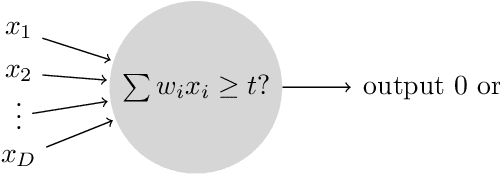
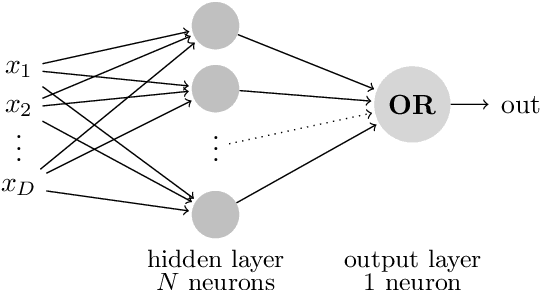
We consider a simple setting in neuroevolution where an evolutionary algorithm optimizes the weights and activation functions of a simple artificial neural network. We then define simple example functions to be learned by the network and conduct rigorous runtime analyses for networks with a single neuron and for a more advanced structure with several neurons and two layers. Our results show that the proposed algorithm is generally efficient on two example problems designed for one neuron and efficient with at least constant probability on the example problem for a two-layer network. In particular, the so-called harmonic mutation operator choosing steps of size $j$ with probability proportional to $1/j$ turns out as a good choice for the underlying search space. However, for the case of one neuron, we also identify situations with hard-to-overcome local optima. Experimental investigations of our neuroevolutionary algorithm and a state-of-the-art CMA-ES support the theoretical findings.

Fast Pareto Optimization Using Sliding Window Selection

Pareto optimization using evolutionary multi-objective algorithms has been widely applied to solve constrained submodular optimization problems. A crucial factor determining the runtime of the used evolutionary algorithms to obtain good approximations is the population size of the algorithms which grows with the number of trade-offs that the algorithms encounter. In this paper, we introduce a sliding window speed up technique for recently introduced algorithms. We prove that our technique eliminates the population size as a crucial factor negatively impacting the runtime and achieves the same theoretical performance guarantees as previous approaches within less computation time. Our experimental investigations for the classical maximum coverage problem confirms that our sliding window technique clearly leads to better results for a wide range of instances and constraint settings.

3-Objective Pareto Optimization for Problems with Chance Constraints

Evolutionary multi-objective algorithms have successfully been used in the context of Pareto optimization where a given constraint is relaxed into an additional objective. In this paper, we explore the use of 3-objective formulations for problems with chance constraints. Our formulation trades off the expected cost and variance of the stochastic component as well as the given deterministic constraint. We point out benefits that this 3-objective formulation has compared to a bi-objective one recently investigated for chance constraints with Normally distributed stochastic components. Our analysis shows that the 3-objective formulation allows to compute all required trade-offs using 1-bit flips only, when dealing with a deterministic cardinality constraint. Furthermore, we carry out experimental investigations for the chance constrained dominating set problem and show the benefit for this classical NP-hard problem.

Runtime Analysis of the EA on Weighted Sums of Transformed Linear Functions

Linear functions play a key role in the runtime analysis of evolutionary algorithms and studies have provided a wide range of new insights and techniques for analyzing evolutionary computation methods. Motivated by studies on separable functions and the optimization behaviour of evolutionary algorithms as well as objective functions from the area of chance constrained optimization, we study the class of objective functions that are weighted sums of two transformed linear functions. Our results show that the (1+1) EA, with a mutation rate depending on the number of overlapping bits of the functions, obtains an optimal solution for these functions in expected time O(n log n), thereby generalizing a well-known result for linear functions to a much wider range of problems.

The Compact Genetic Algorithm Struggles on Cliff Functions

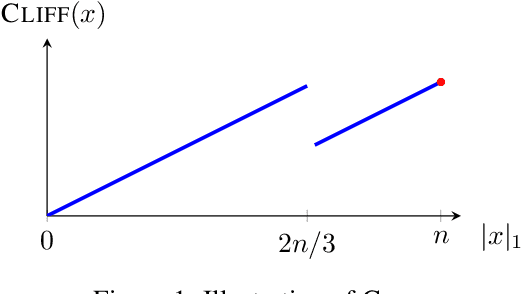
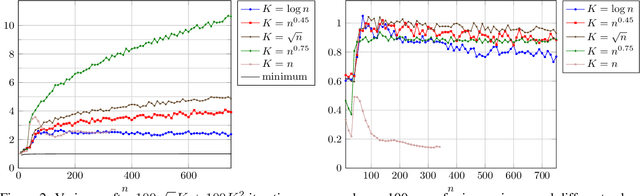
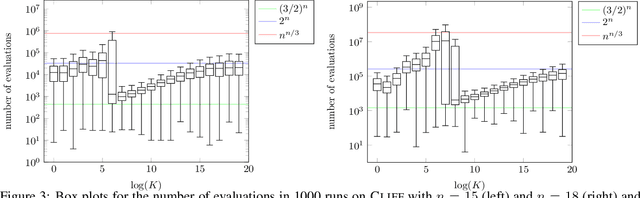
The compact genetic algorithm (cGA) is an non-elitist estimation of distribution algorithm which has shown to be able to deal with difficult multimodal fitness landscapes that are hard to solve by elitist algorithms. In this paper, we investigate the cGA on the CLIFF function for which it has been shown recently that non-elitist evolutionary algorithms and artificial immune systems optimize it in expected polynomial time. We point out that the cGA faces major difficulties when solving the CLIFF function and investigate its dynamics both experimentally and theoretically around the cliff. Our experimental results indicate that the cGA requires exponential time for all values of the update strength $K$. We show theoretically that, under sensible assumptions, there is a negative drift when sampling around the location of the cliff. Experiments further suggest that there is a phase transition for $K$ where the expected optimization time drops from $n^{\Theta(n)}$ to $2^{\Theta(n)}$.

Simulated Annealing is a Polynomial-Time Approximation Scheme for the Minimum Spanning Tree Problem

We prove that Simulated Annealing with an appropriate cooling schedule computes arbitrarily tight constant-factor approximations to the minimum spanning tree problem in polynomial time. This result was conjectured by Wegener (2005). More precisely, denoting by $n, m, w_{\max}$, and $w_{\min}$ the number of vertices and edges as well as the maximum and minimum edge weight of the MST instance, we prove that simulated annealing with initial temperature $T_0 \ge w_{\max}$ and multiplicative cooling schedule with factor $1-1/\ell$, where $\ell = \omega (mn\ln(m))$, with probability at least $1-1/m$ computes in time $O(\ell (\ln\ln (\ell) + \ln(T_0/w_{\min}) ))$ a spanning tree with weight at most $1+\kappa$ times the optimum weight, where $1+\kappa = \frac{(1+o(1))\ln(\ell m)}{\ln(\ell) -\ln (mn\ln (m))}$. Consequently, for any $\epsilon>0$, we can choose $\ell$ in such a way that a $(1+\epsilon)$-approximation is found in time $O((mn\ln(n))^{1+1/\epsilon+o(1)}(\ln\ln n + \ln(T_0/w_{\min})))$ with probability at least $1-1/m$. In the special case of so-called $(1+\epsilon)$-separated weights, this algorithm computes an optimal solution (again in time $O( (mn\ln(n))^{1+1/\epsilon+o(1)}(\ln\ln n + \ln(T_0/w_{\min})))$), which is a significant speed-up over Wegener's runtime guarantee of $O(m^{8 + 8/\epsilon})$.