The Compact Genetic Algorithm Struggles on Cliff Functions
Paper and Code
Apr 11, 2022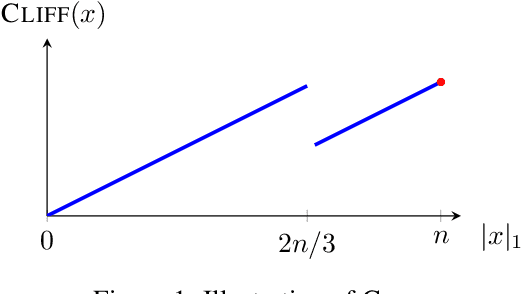
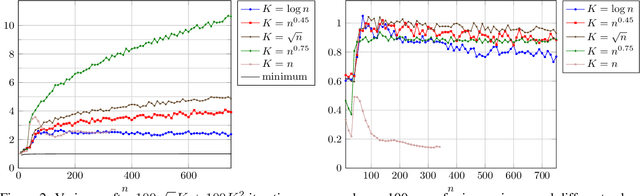
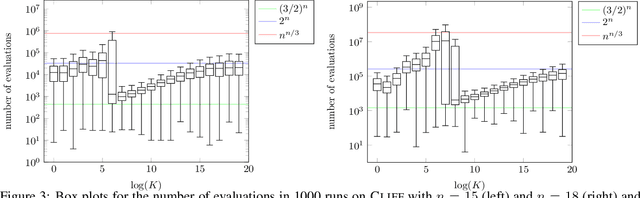
The compact genetic algorithm (cGA) is an non-elitist estimation of distribution algorithm which has shown to be able to deal with difficult multimodal fitness landscapes that are hard to solve by elitist algorithms. In this paper, we investigate the cGA on the CLIFF function for which it has been shown recently that non-elitist evolutionary algorithms and artificial immune systems optimize it in expected polynomial time. We point out that the cGA faces major difficulties when solving the CLIFF function and investigate its dynamics both experimentally and theoretically around the cliff. Our experimental results indicate that the cGA requires exponential time for all values of the update strength $K$. We show theoretically that, under sensible assumptions, there is a negative drift when sampling around the location of the cliff. Experiments further suggest that there is a phase transition for $K$ where the expected optimization time drops from $n^{\Theta(n)}$ to $2^{\Theta(n)}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge