Artificial Immune Systems Can Find Arbitrarily Good Approximations for the NP-Hard Partition Problem

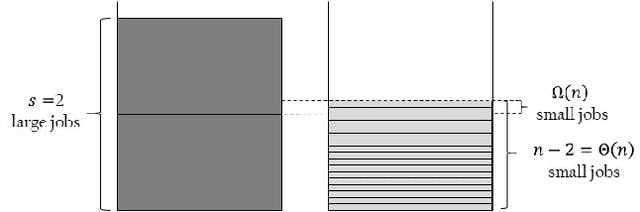
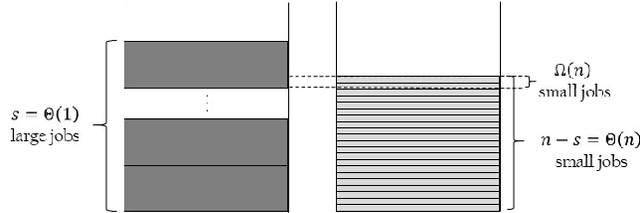
Typical Artificial Immune System (AIS) operators such as hypermutations with mutation potential and ageing allow to efficiently overcome local optima from which Evolutionary Algorithms (EAs) struggle to escape. Such behaviour has been shown for artificial example functions such as Jump, Cliff or Trap constructed especially to show difficulties that EAs may encounter during the optimisation process. However, no evidence is available indicating that similar effects may also occur in more realistic problems. In this paper we perform an analysis for the standard NP-Hard \partition problem from combinatorial optimisation and rigorously show that hypermutations and ageing allow AISs to efficiently escape from local optima where standard EAs require exponential time. As a result we prove that while EAs and Random Local Search may get trapped on 4/3 approximations, AISs find arbitrarily good approximate solutions of ratio (1+$\epsilon$) for any constant $\epsilon$ within a time that is polynomial in the problem size and exponential only in $1/\epsilon$.