On Inversely Proportional Hypermutations with Mutation Potential

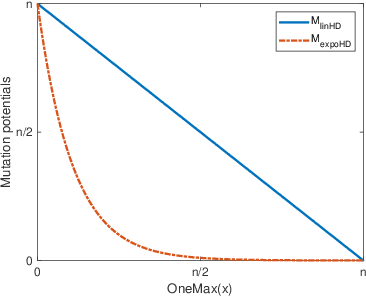
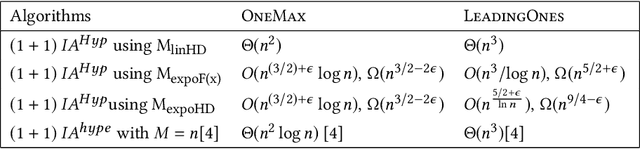
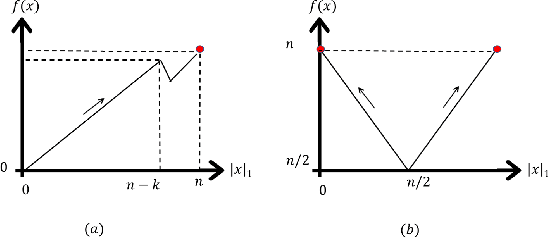
Artificial Immune Systems (AIS) employing hypermutations with linear static mutation potential have recently been shown to be very effective at escaping local optima of combinatorial optimisation problems at the expense of being slower during the exploitation phase compared to standard evolutionary algorithms. In this paper we prove that considerable speed-ups in the exploitation phase may be achieved with dynamic inversely proportional mutation potentials (IPM) and argue that the potential should decrease inversely to the distance to the optimum rather than to the difference in fitness. Afterwards we define a simple (1+1)~Opt-IA, that uses IPM hypermutations and ageing, for realistic applications where optimal solutions are unknown. The aim of the AIS is to approximate the ideal behaviour of the inversely proportional hypermutations better and better as the search space is explored. We prove that such desired behaviour, and related speed-ups, occur for a well-studied bimodal benchmark function called \textsc{TwoMax}. Furthermore, we prove that the (1+1)~Opt-IA with IPM efficiently optimises a third bimodal function, \textsc{Cliff}, by escaping its local optima while Opt-IA with static potential cannot, thus requires exponential expected runtime in the distance between the cliff and the optimum.

Artificial Immune Systems Can Find Arbitrarily Good Approximations for the NP-Hard Partition Problem

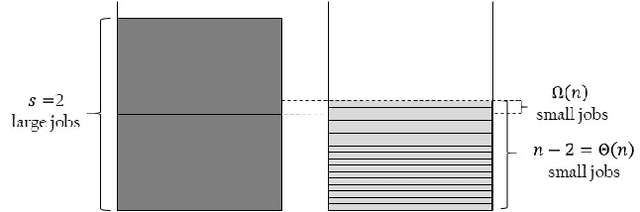
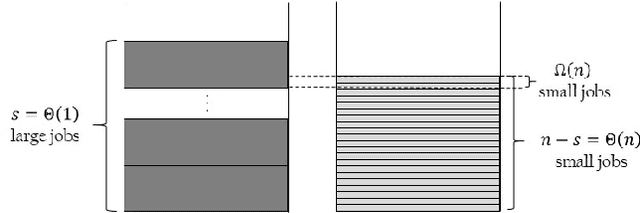
Typical Artificial Immune System (AIS) operators such as hypermutations with mutation potential and ageing allow to efficiently overcome local optima from which Evolutionary Algorithms (EAs) struggle to escape. Such behaviour has been shown for artificial example functions such as Jump, Cliff or Trap constructed especially to show difficulties that EAs may encounter during the optimisation process. However, no evidence is available indicating that similar effects may also occur in more realistic problems. In this paper we perform an analysis for the standard NP-Hard \partition problem from combinatorial optimisation and rigorously show that hypermutations and ageing allow AISs to efficiently escape from local optima where standard EAs require exponential time. As a result we prove that while EAs and Random Local Search may get trapped on 4/3 approximations, AISs find arbitrarily good approximate solutions of ratio (1+$\epsilon$) for any constant $\epsilon$ within a time that is polynomial in the problem size and exponential only in $1/\epsilon$.

Fast Artificial Immune Systems

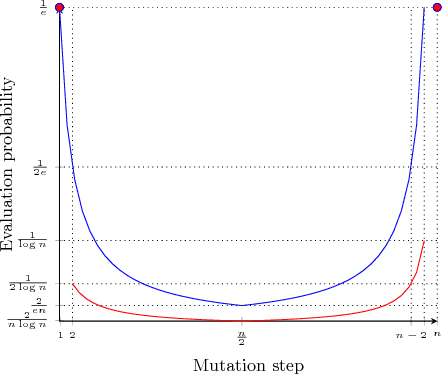
Various studies have shown that characteristic Artificial Immune System (AIS) operators such as hypermutations and ageing can be very efficient at escaping local optima of multimodal optimisation problems. However, this efficiency comes at the expense of considerably slower runtimes during the exploitation phase compared to standard evolutionary algorithms. We propose modifications to the traditional `hypermutations with mutation potential' (HMP) that allow them to be efficient at exploitation as well as maintaining their effective explorative characteristics. Rather than deterministically evaluating fitness after each bitflip of a hypermutation, we sample the fitness function stochastically with a `parabolic' distribution which allows the `stop at first constructive mutation' (FCM) variant of HMP to reduce the linear amount of wasted function evaluations when no improvement is found to a constant. By returning the best sampled solution during the hypermutation, rather than the first constructive mutation, we then turn the extremely inefficient HMP operator without FCM, into a very effective operator for the standard Opt-IA AIS using hypermutation, cloning and ageing. We rigorously prove the effectiveness of the two proposed operators by analysing them on all problems where the performance of HPM is rigorously understood in the literature. %

When Hypermutations and Ageing Enable Artificial Immune Systems to Outperform Evolutionary Algorithms

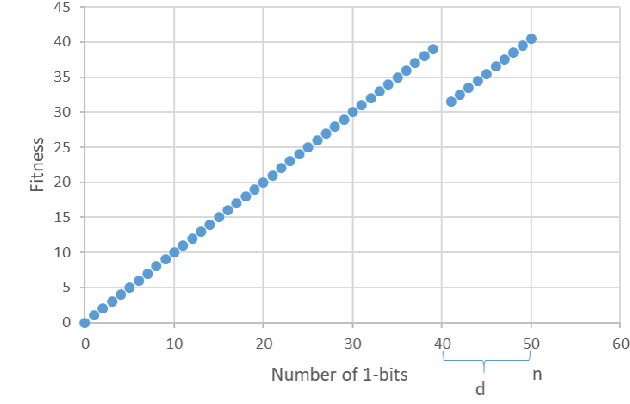
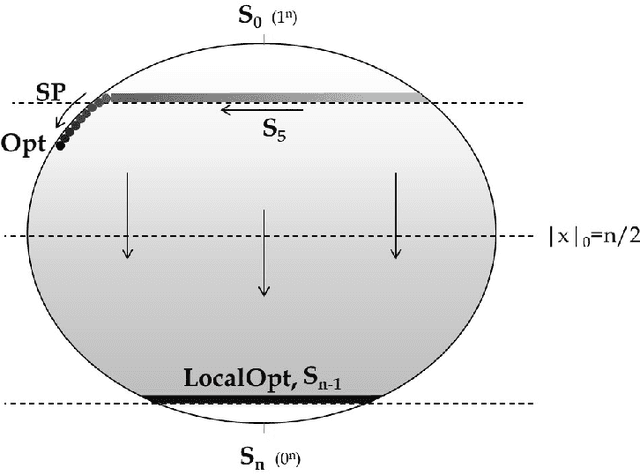
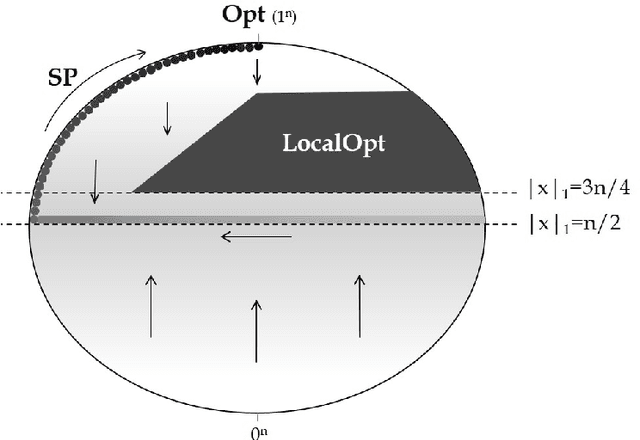
We present a time complexity analysis of the Opt-IA artificial immune system (AIS). We first highlight the power and limitations of its distinguishing operators (i.e., hypermutations with mutation potential and ageing) by analysing them in isolation. Recent work has shown that ageing combined with local mutations can help escape local optima on a dynamic optimisation benchmark function. We generalise this result by rigorously proving that, compared to evolutionary algorithms (EAs), ageing leads to impressive speed-ups on the standard Cliff benchmark function both when using local and global mutations. Unless the stop at first constructive mutation (FCM) mechanism is applied, we show that hypermutations require exponential expected runtime to optimise any function with a polynomial number of optima. If instead FCM is used, the expected runtime is at most a linear factor larger than the upper bound achieved for any random local search algorithm using the artificial fitness levels method. Nevertheless, we prove that algorithms using hypermutations can be considerably faster than EAs at escaping local optima. An analysis of the complete Opt-IA reveals that it is efficient on the previously considered functions and highlights problems where the use of the full algorithm is crucial. We complete the picture by presenting a class of functions for which Opt-IA fails with overwhelming probability while standard EAs are efficient.