When Hypermutations and Ageing Enable Artificial Immune Systems to Outperform Evolutionary Algorithms
Paper and Code
Apr 04, 2018
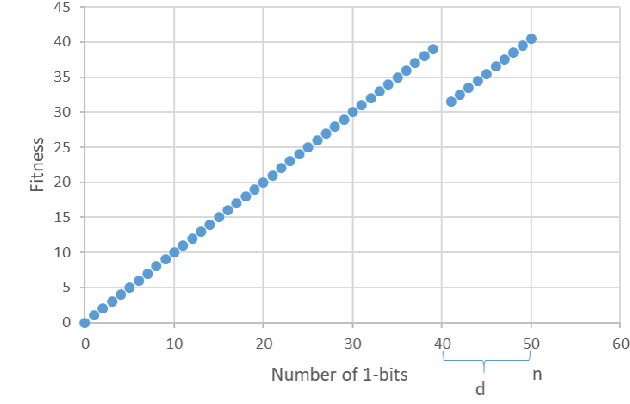
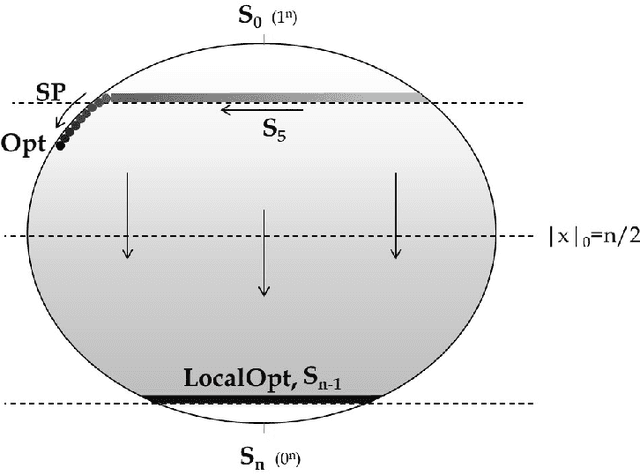
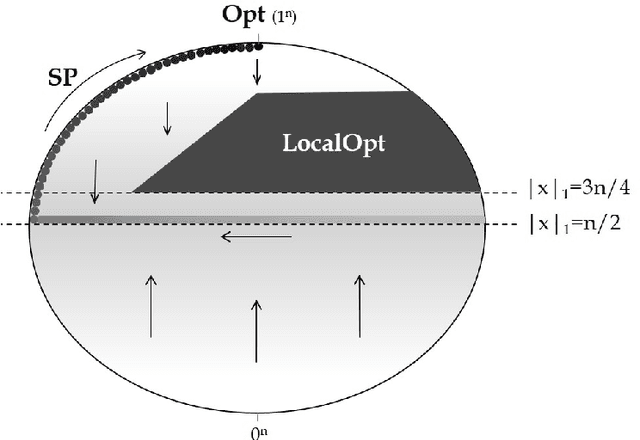
We present a time complexity analysis of the Opt-IA artificial immune system (AIS). We first highlight the power and limitations of its distinguishing operators (i.e., hypermutations with mutation potential and ageing) by analysing them in isolation. Recent work has shown that ageing combined with local mutations can help escape local optima on a dynamic optimisation benchmark function. We generalise this result by rigorously proving that, compared to evolutionary algorithms (EAs), ageing leads to impressive speed-ups on the standard Cliff benchmark function both when using local and global mutations. Unless the stop at first constructive mutation (FCM) mechanism is applied, we show that hypermutations require exponential expected runtime to optimise any function with a polynomial number of optima. If instead FCM is used, the expected runtime is at most a linear factor larger than the upper bound achieved for any random local search algorithm using the artificial fitness levels method. Nevertheless, we prove that algorithms using hypermutations can be considerably faster than EAs at escaping local optima. An analysis of the complete Opt-IA reveals that it is efficient on the previously considered functions and highlights problems where the use of the full algorithm is crucial. We complete the picture by presenting a class of functions for which Opt-IA fails with overwhelming probability while standard EAs are efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge