Hardest Monotone Functions for Evolutionary Algorithms

The study of hardest and easiest fitness landscapes is an active area of research. Recently, Kaufmann, Larcher, Lengler and Zou conjectured that for the self-adjusting $(1,\lambda)$-EA, Adversarial Dynamic BinVal (ADBV) is the hardest dynamic monotone function to optimize. We introduce the function Switching Dynamic BinVal (SDBV) which coincides with ADBV whenever the number of remaining zeros in the search point is strictly less than $n/2$, where $n$ denotes the dimension of the search space. We show, using a combinatorial argument, that for the $(1+1)$-EA with any mutation rate $p \in [0,1]$, SDBV is drift-minimizing among the class of dynamic monotone functions. Our construction provides the first explicit example of an instance of the partially-ordered evolutionary algorithm (PO-EA) model with parameterized pessimism introduced by Colin, Doerr and F\'erey, building on work of Jansen. We further show that the $(1+1)$-EA optimizes SDBV in $\Theta(n^{3/2})$ generations. Our simulations demonstrate matching runtimes for both static and self-adjusting $(1,\lambda)$ and $(1+\lambda)$-EA. We further show, using an example of fixed dimension, that drift-minimization does not equal maximal runtime.

Gated recurrent neural networks discover attention

Recent architectural developments have enabled recurrent neural networks (RNNs) to reach and even surpass the performance of Transformers on certain sequence modeling tasks. These modern RNNs feature a prominent design pattern: linear recurrent layers interconnected by feedforward paths with multiplicative gating. Here, we show how RNNs equipped with these two design elements can exactly implement (linear) self-attention, the main building block of Transformers. By reverse-engineering a set of trained RNNs, we find that gradient descent in practice discovers our construction. In particular, we examine RNNs trained to solve simple in-context learning tasks on which Transformers are known to excel and find that gradient descent instills in our RNNs the same attention-based in-context learning algorithm used by Transformers. Our findings highlight the importance of multiplicative interactions in neural networks and suggest that certain RNNs might be unexpectedly implementing attention under the hood.

OneMax is not the Easiest Function for Fitness Improvements

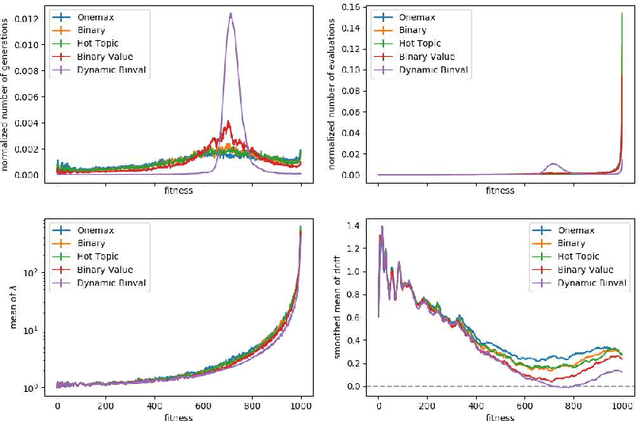
We study the $(1:s+1)$ success rule for controlling the population size of the $(1,\lambda)$-EA. It was shown by Hevia Fajardo and Sudholt that this parameter control mechanism can run into problems for large $s$ if the fitness landscape is too easy. They conjectured that this problem is worst for the OneMax benchmark, since in some well-established sense OneMax is known to be the easiest fitness landscape. In this paper we disprove this conjecture and show that OneMax is not the easiest fitness landscape with respect to finding improving steps. As a consequence, we show that there exists $s$ and $\varepsilon$ such that the self-adjusting $(1,\lambda)$-EA with $(1:s+1)$-rule optimizes OneMax efficiently when started with $\varepsilon n$ zero-bits, but does not find the optimum in polynomial time on Dynamic BinVal. Hence, we show that there are landscapes where the problem of the $(1:s+1)$-rule for controlling the population size of the $(1, \lambda)$-EA is more severe than for OneMax.

Self-adjusting Population Sizes for the $$-EA on Monotone Functions

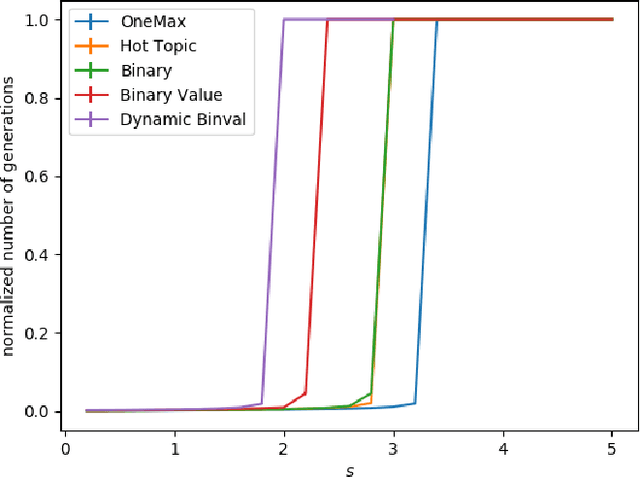
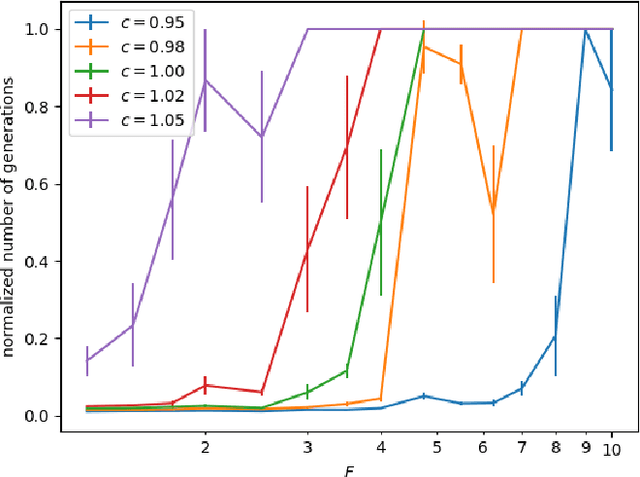
We study the $(1,\lambda)$-EA with mutation rate $c/n$ for $c\le 1$, where the population size is adaptively controlled with the $(1:s+1)$-success rule. Recently, Hevia Fajardo and Sudholt have shown that this setup with $c=1$ is efficient on \onemax for $s<1$, but inefficient if $s \ge 18$. Surprisingly, the hardest part is not close to the optimum, but rather at linear distance. We show that this behavior is not specific to \onemax. If $s$ is small, then the algorithm is efficient on all monotone functions, and if $s$ is large, then it needs superpolynomial time on all monotone functions. In the former case, for $c<1$ we show a $O(n)$ upper bound for the number of generations and $O(n\log n)$ for the number of function evaluations, and for $c=1$ we show $O(n\log n)$ generations and $O(n^2\log\log n)$ evaluations. We also show formally that optimization is always fast, regardless of $s$, if the algorithm starts in proximity of the optimum. All results also hold in a dynamic environment where the fitness function changes in each generation.