OneMax is not the Easiest Function for Fitness Improvements
Paper and Code
Apr 14, 2022
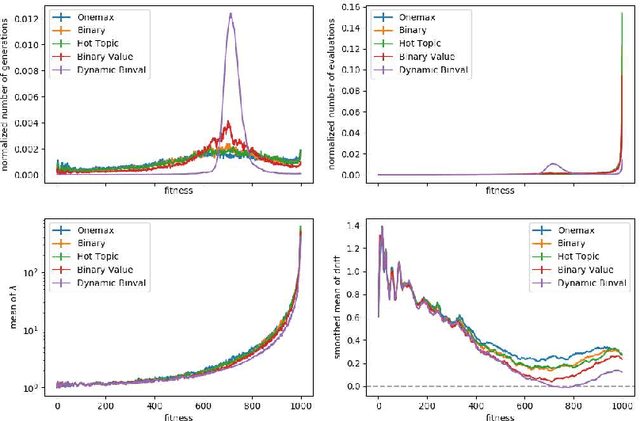
We study the $(1:s+1)$ success rule for controlling the population size of the $(1,\lambda)$-EA. It was shown by Hevia Fajardo and Sudholt that this parameter control mechanism can run into problems for large $s$ if the fitness landscape is too easy. They conjectured that this problem is worst for the OneMax benchmark, since in some well-established sense OneMax is known to be the easiest fitness landscape. In this paper we disprove this conjecture and show that OneMax is not the easiest fitness landscape with respect to finding improving steps. As a consequence, we show that there exists $s$ and $\varepsilon$ such that the self-adjusting $(1,\lambda)$-EA with $(1:s+1)$-rule optimizes OneMax efficiently when started with $\varepsilon n$ zero-bits, but does not find the optimum in polynomial time on Dynamic BinVal. Hence, we show that there are landscapes where the problem of the $(1:s+1)$-rule for controlling the population size of the $(1, \lambda)$-EA is more severe than for OneMax.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge