Xun Zou
MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention
Jun 16, 2025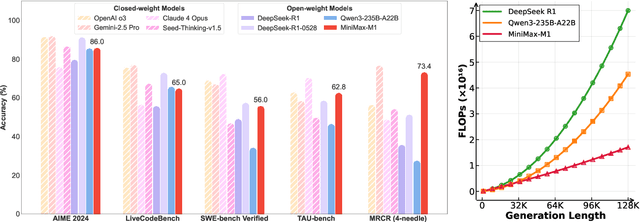

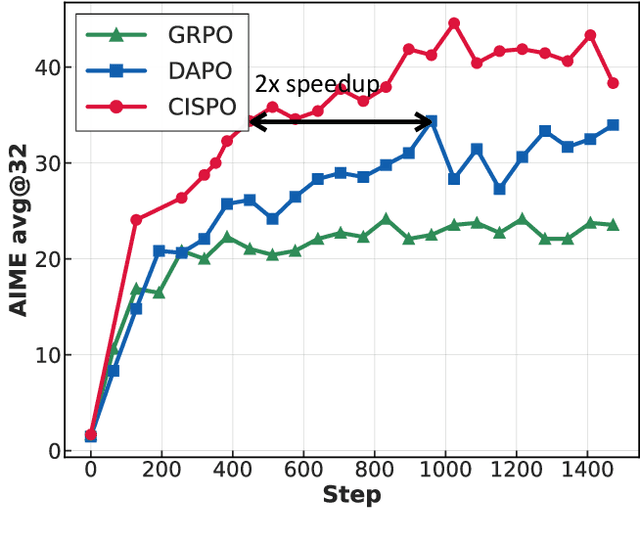
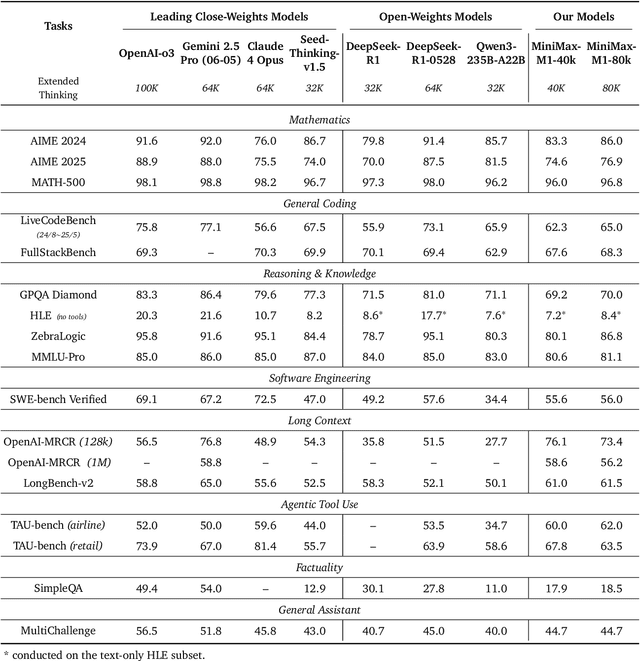
Abstract:We introduce MiniMax-M1, the world's first open-weight, large-scale hybrid-attention reasoning model. MiniMax-M1 is powered by a hybrid Mixture-of-Experts (MoE) architecture combined with a lightning attention mechanism. The model is developed based on our previous MiniMax-Text-01 model, which contains a total of 456 billion parameters with 45.9 billion parameters activated per token. The M1 model natively supports a context length of 1 million tokens, 8x the context size of DeepSeek R1. Furthermore, the lightning attention mechanism in MiniMax-M1 enables efficient scaling of test-time compute. These properties make M1 particularly suitable for complex tasks that require processing long inputs and thinking extensively. MiniMax-M1 is trained using large-scale reinforcement learning (RL) on diverse problems including sandbox-based, real-world software engineering environments. In addition to M1's inherent efficiency advantage for RL training, we propose CISPO, a novel RL algorithm to further enhance RL efficiency. CISPO clips importance sampling weights rather than token updates, outperforming other competitive RL variants. Combining hybrid-attention and CISPO enables MiniMax-M1's full RL training on 512 H800 GPUs to complete in only three weeks, with a rental cost of just $534,700. We release two versions of MiniMax-M1 models with 40K and 80K thinking budgets respectively, where the 40K model represents an intermediate phase of the 80K training. Experiments on standard benchmarks show that our models are comparable or superior to strong open-weight models such as the original DeepSeek-R1 and Qwen3-235B, with particular strengths in complex software engineering, tool utilization, and long-context tasks. We publicly release MiniMax-M1 at https://github.com/MiniMax-AI/MiniMax-M1.
MiniMax-01: Scaling Foundation Models with Lightning Attention
Jan 14, 2025Abstract:We introduce MiniMax-01 series, including MiniMax-Text-01 and MiniMax-VL-01, which are comparable to top-tier models while offering superior capabilities in processing longer contexts. The core lies in lightning attention and its efficient scaling. To maximize computational capacity, we integrate it with Mixture of Experts (MoE), creating a model with 32 experts and 456 billion total parameters, of which 45.9 billion are activated for each token. We develop an optimized parallel strategy and highly efficient computation-communication overlap techniques for MoE and lightning attention. This approach enables us to conduct efficient training and inference on models with hundreds of billions of parameters across contexts spanning millions of tokens. The context window of MiniMax-Text-01 can reach up to 1 million tokens during training and extrapolate to 4 million tokens during inference at an affordable cost. Our vision-language model, MiniMax-VL-01 is built through continued training with 512 billion vision-language tokens. Experiments on both standard and in-house benchmarks show that our models match the performance of state-of-the-art models like GPT-4o and Claude-3.5-Sonnet while offering 20-32 times longer context window. We publicly release MiniMax-01 at https://github.com/MiniMax-AI.
OneMax is not the Easiest Function for Fitness Improvements
Apr 14, 2022
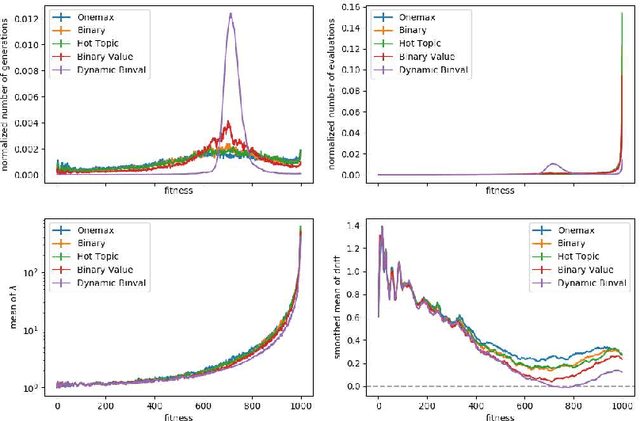
Abstract:We study the $(1:s+1)$ success rule for controlling the population size of the $(1,\lambda)$-EA. It was shown by Hevia Fajardo and Sudholt that this parameter control mechanism can run into problems for large $s$ if the fitness landscape is too easy. They conjectured that this problem is worst for the OneMax benchmark, since in some well-established sense OneMax is known to be the easiest fitness landscape. In this paper we disprove this conjecture and show that OneMax is not the easiest fitness landscape with respect to finding improving steps. As a consequence, we show that there exists $s$ and $\varepsilon$ such that the self-adjusting $(1,\lambda)$-EA with $(1:s+1)$-rule optimizes OneMax efficiently when started with $\varepsilon n$ zero-bits, but does not find the optimum in polynomial time on Dynamic BinVal. Hence, we show that there are landscapes where the problem of the $(1:s+1)$-rule for controlling the population size of the $(1, \lambda)$-EA is more severe than for OneMax.
Self-adjusting Population Sizes for the $$-EA on Monotone Functions
Apr 01, 2022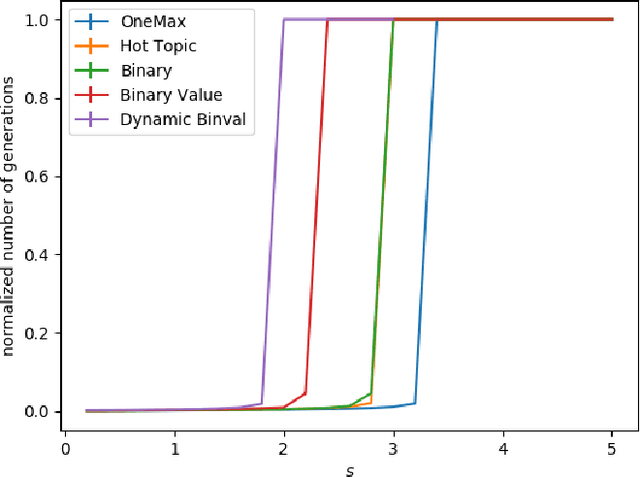
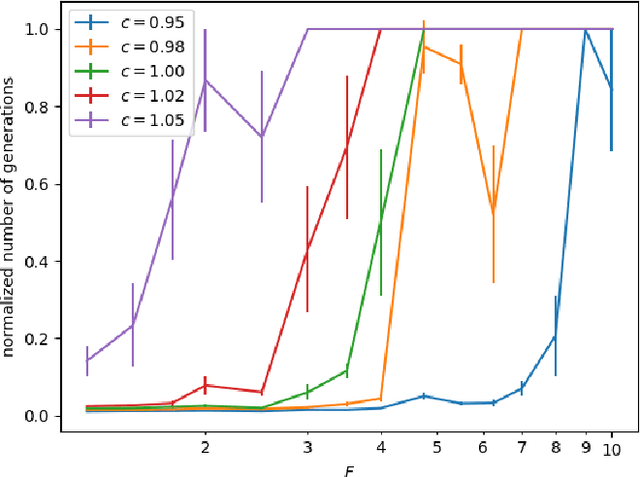
Abstract:We study the $(1,\lambda)$-EA with mutation rate $c/n$ for $c\le 1$, where the population size is adaptively controlled with the $(1:s+1)$-success rule. Recently, Hevia Fajardo and Sudholt have shown that this setup with $c=1$ is efficient on \onemax for $s<1$, but inefficient if $s \ge 18$. Surprisingly, the hardest part is not close to the optimum, but rather at linear distance. We show that this behavior is not specific to \onemax. If $s$ is small, then the algorithm is efficient on all monotone functions, and if $s$ is large, then it needs superpolynomial time on all monotone functions. In the former case, for $c<1$ we show a $O(n)$ upper bound for the number of generations and $O(n\log n)$ for the number of function evaluations, and for $c=1$ we show $O(n\log n)$ generations and $O(n^2\log\log n)$ evaluations. We also show formally that optimization is always fast, regardless of $s$, if the algorithm starts in proximity of the optimum. All results also hold in a dynamic environment where the fitness function changes in each generation.
Molecular modeling with machine-learned universal potential functions
Mar 06, 2021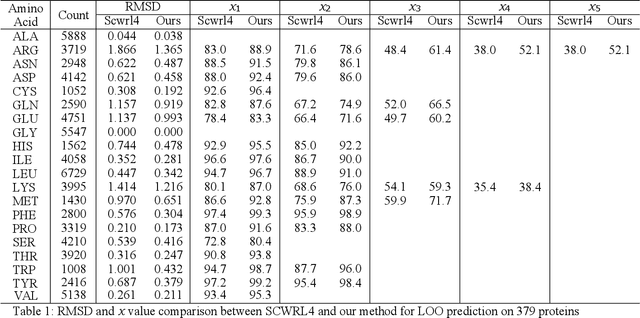


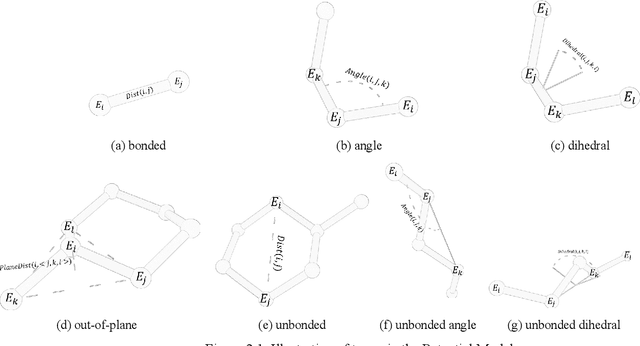
Abstract:Molecular modeling is an important topic in drug discovery. Decades of research have led to the development of high quality scalable molecular force fields. In this paper, we show that neural networks can be used to train an universal approximator for energy potential functions. By incorporating a fully automated training process we have been able to train smooth, differentiable, and predictive potential functions on large scale crystal structures. A variety of tests have also performed to show the superiority and versatility of the machine-learned model.
Exponential Slowdown for Larger Populations: The $(μ+1)$-EA on Monotone Functions
Jul 30, 2019Abstract:Pseudo-Boolean monotone functions are unimodal functions which are trivial to optimize for some hillclimbers, but are challenging for a surprising number of evolutionary algorithms (EAs). A general trend is that EAs are efficient if parameters like the mutation rate are set conservatively, but may need exponential time otherwise. In particular, it was known that the $(1+1)$-EA and the $(1+\lambda)$-EA can optimize every monotone function in pseudolinear time if the mutation rate is $c/n$ for some $c<1$, but they need exponential time for some monotone functions for $c>2.2$. The second part of the statement was also known for the $(\mu+1)$-EA. In this paper we show that the first statement does not apply to the $(\mu+1)$-EA. More precisely, we prove that for every constant $c>0$ there is a constant integer $\mu_0$ such that the $(\mu+1)$-EA with mutation rate $c/n$ and population size $\mu_0\le\mu\le n$ needs superpolynomial time to optimize some monotone functions. Thus, increasing the population size by just a constant has devastating effects on the performance. This is in stark contrast to many other benchmark functions on which increasing the population size either increases the performance significantly, or affects performance mildly. The reason why larger populations are harmful lies in the fact that larger populations may temporarily decrease selective pressure on parts of the population. This allows unfavorable mutations to accumulate in single individuals and their descendants. If the population moves sufficiently fast through the search space, such unfavorable descendants can become ancestors of future generations, and the bad mutations are preserved. Remarkably, this effect only occurs if the population renews itself sufficiently fast, which can only happen far away from the optimum. This is counter-intuitive since usually optimization gets harder as we approach the optimum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge