Optimal Kronecker-Sum Approximation of Real Time Recurrent Learning

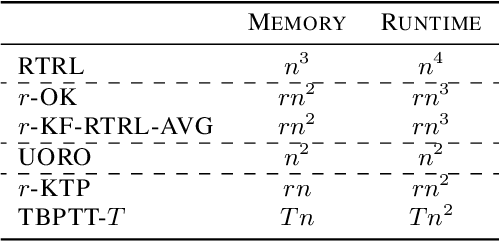
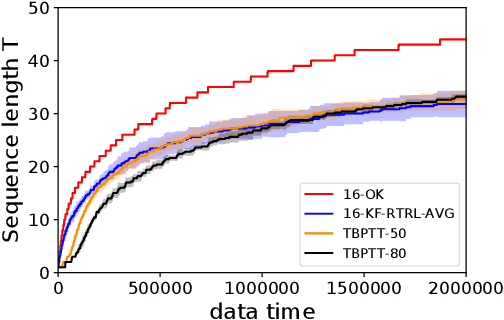
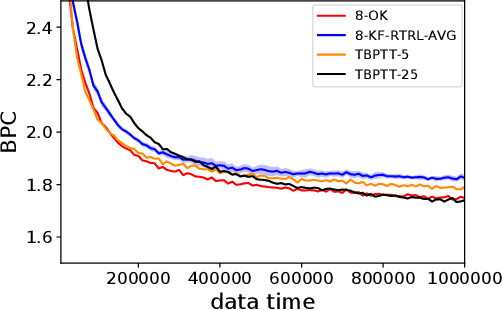
One of the central goals of Recurrent Neural Networks (RNNs) is to learn long-term dependencies in sequential data. Nevertheless, the most popular training method, Truncated Backpropagation through Time (TBPTT), categorically forbids learning dependencies beyond the truncation horizon. In contrast, the online training algorithm Real Time Recurrent Learning (RTRL) provides untruncated gradients, with the disadvantage of impractically large computational costs. Recently published approaches reduce these costs by providing noisy approximations of RTRL. We present a new approximation algorithm of RTRL, Optimal Kronecker-Sum Approximation (OK). We prove that OK is optimal for a class of approximations of RTRL, which includes all approaches published so far. Additionally, we show that OK has empirically negligible noise: Unlike previous algorithms it matches TBPTT in a real world task (character-level Penn TreeBank) and can exploit online parameter updates to outperform TBPTT in a synthetic string memorization task.

When Does Hillclimbing Fail on Monotone Functions: An entropy compression argument

Hillclimbing is an essential part of any optimization algorithm. An important benchmark for hillclimbing algorithms on pseudo-Boolean functions $f: \{0,1\}^n \to \mathbb{R}$ are (strictly) montone functions, on which a surprising number of hillclimbers fail to be efficient. For example, the $(1+1)$-Evolutionary Algorithm is a standard hillclimber which flips each bit independently with probability $c/n$ in each round. Perhaps surprisingly, this algorithm shows a phase transition: it optimizes any monotone pseudo-boolean function in quasilinear time if $c<1$, but there are monotone functions for which the algorithm needs exponential time if $c>2.2$. But so far it was unclear whether the threshold is at $c=1$. In this paper we show how Moser's entropy compression argument can be adapted to this situation, that is, we show that a long runtime would allow us to encode the random steps of the algorithm with less bits than their entropy. Thus there exists a $c_0 > 1$ such that for all $0<c\le c_0$ the $(1+1)$-Evolutionary Algorithm with rate $c/n$ finds the optimum in $O(n \log^2 n)$ steps in expectation.

A variant of the multi-agent rendezvous problem

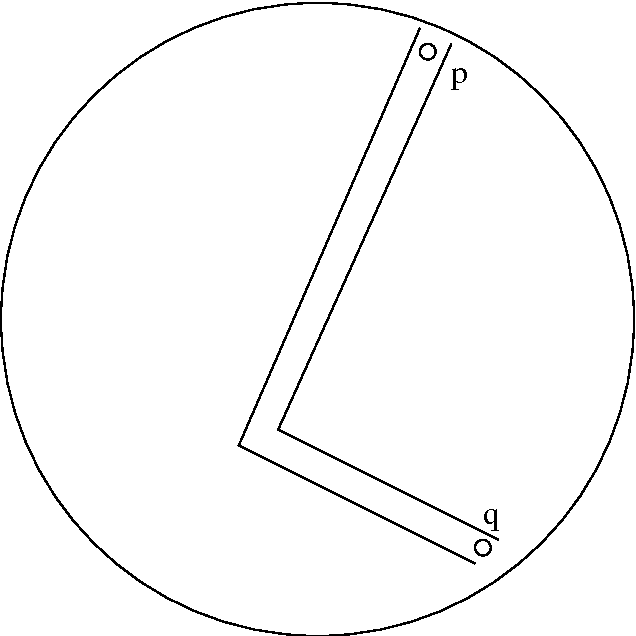
The classical multi-agent rendezvous problem asks for a deterministic algorithm by which $n$ points scattered in a plane can move about at constant speed and merge at a single point, assuming each point can use only the locations of the others it sees when making decisions and that the visibility graph as a whole is connected. In time complexity analyses of such algorithms, only the number of rounds of computation required are usually considered, not the amount of computation done per round. In this paper, we consider $\Omega(n^2 \log n)$ points distributed independently and uniformly at random in a disc of radius $n$ and, assuming each point can not only see but also, in principle, communicate with others within unit distance, seek a randomised merging algorithm which asymptotically almost surely (a.a.s.) runs in time O(n), in other words in time linear in the radius of the disc rather than in the number of points. Under a precise set of assumptions concerning the communication capabilities of neighboring points, we describe an algorithm which a.a.s. runs in time O(n) provided the number of points is $o(n^3)$. Several questions are posed for future work.