Peter Hegarty
A variant of the multi-agent rendezvous problem
Jun 21, 2013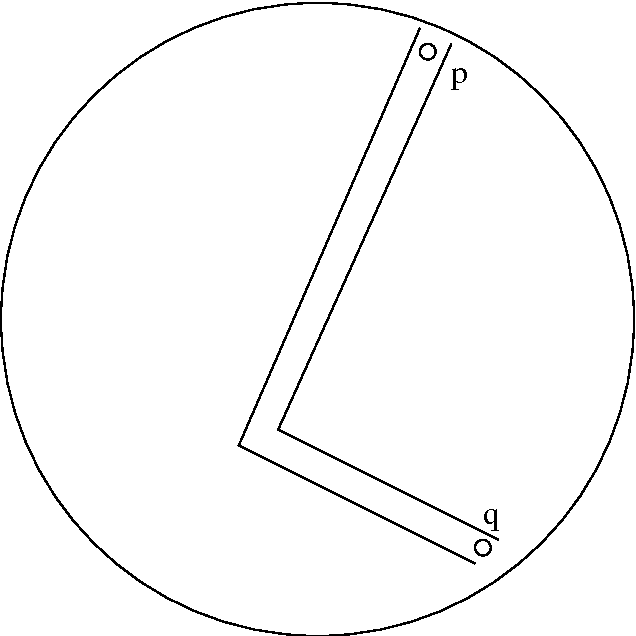
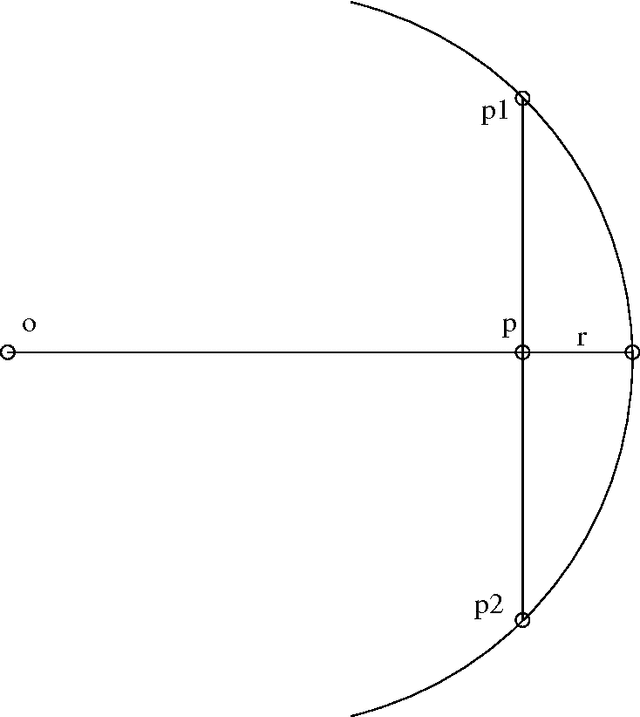
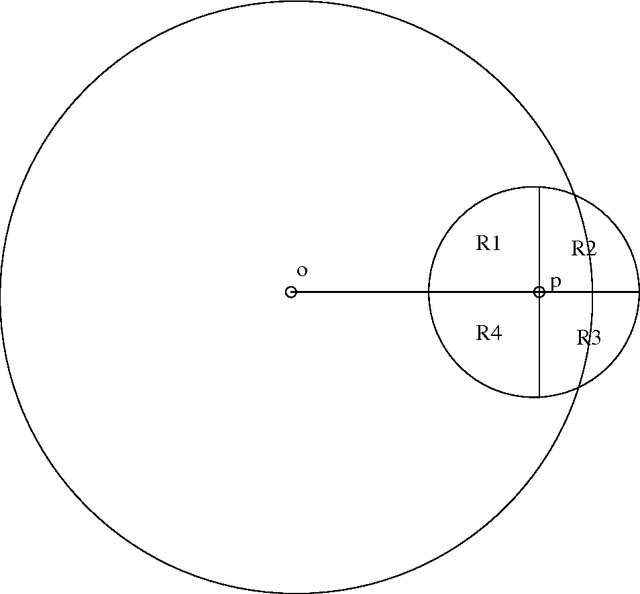
Abstract:The classical multi-agent rendezvous problem asks for a deterministic algorithm by which $n$ points scattered in a plane can move about at constant speed and merge at a single point, assuming each point can use only the locations of the others it sees when making decisions and that the visibility graph as a whole is connected. In time complexity analyses of such algorithms, only the number of rounds of computation required are usually considered, not the amount of computation done per round. In this paper, we consider $\Omega(n^2 \log n)$ points distributed independently and uniformly at random in a disc of radius $n$ and, assuming each point can not only see but also, in principle, communicate with others within unit distance, seek a randomised merging algorithm which asymptotically almost surely (a.a.s.) runs in time O(n), in other words in time linear in the radius of the disc rather than in the number of points. Under a precise set of assumptions concerning the communication capabilities of neighboring points, we describe an algorithm which a.a.s. runs in time O(n) provided the number of points is $o(n^3)$. Several questions are posed for future work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge