Beyond Pairwise Correlations: Higher-Order Redundancies in Self-Supervised Representation Learning

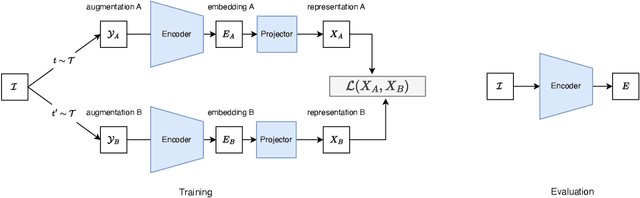
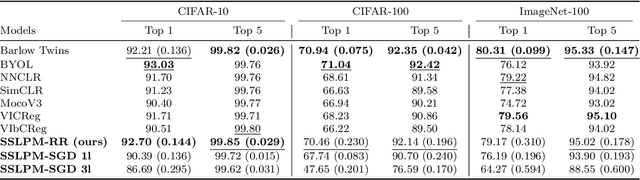
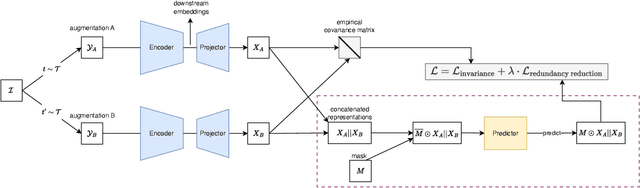
Several self-supervised learning (SSL) approaches have shown that redundancy reduction in the feature embedding space is an effective tool for representation learning. However, these methods consider a narrow notion of redundancy, focusing on pairwise correlations between features. To address this limitation, we formalize the notion of embedding space redundancy and introduce redundancy measures that capture more complex, higher-order dependencies. We mathematically analyze the relationships between these metrics, and empirically measure these redundancies in the embedding spaces of common SSL methods. Based on our findings, we propose Self Supervised Learning with Predictability Minimization (SSLPM) as a method for reducing redundancy in the embedding space. SSLPM combines an encoder network with a predictor engaging in a competitive game of reducing and exploiting dependencies respectively. We demonstrate that SSLPM is competitive with state-of-the-art methods and find that the best performing SSL methods exhibit low embedding space redundancy, suggesting that even methods without explicit redundancy reduction mechanisms perform redundancy reduction implicitly.

Random initialisations performing above chance and how to find them

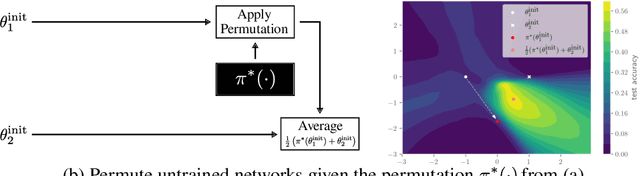
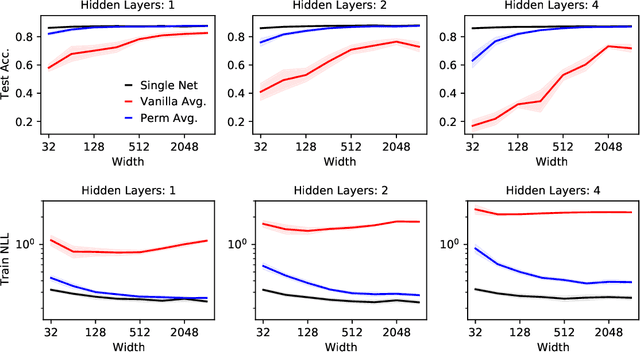
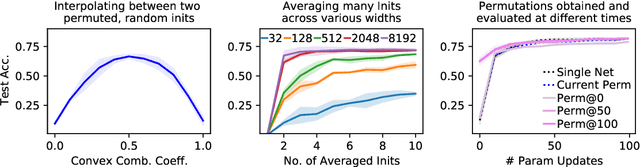
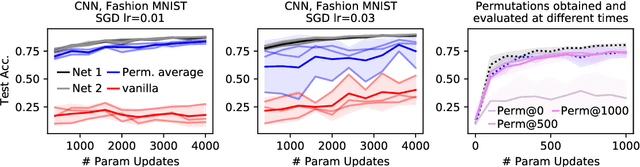
Neural networks trained with stochastic gradient descent (SGD) starting from different random initialisations typically find functionally very similar solutions, raising the question of whether there are meaningful differences between different SGD solutions. Entezari et al. recently conjectured that despite different initialisations, the solutions found by SGD lie in the same loss valley after taking into account the permutation invariance of neural networks. Concretely, they hypothesise that any two solutions found by SGD can be permuted such that the linear interpolation between their parameters forms a path without significant increases in loss. Here, we use a simple but powerful algorithm to find such permutations that allows us to obtain direct empirical evidence that the hypothesis is true in fully connected networks. Strikingly, we find that two networks already live in the same loss valley at the time of initialisation and averaging their random, but suitably permuted initialisation performs significantly above chance. In contrast, for convolutional architectures, our evidence suggests that the hypothesis does not hold. Especially in a large learning rate regime, SGD seems to discover diverse modes.

Gradient Descent on Neurons and its Link to Approximate Second-Order Optimization

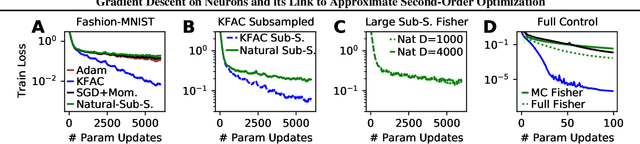
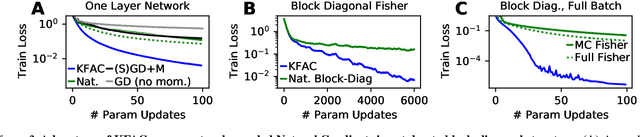
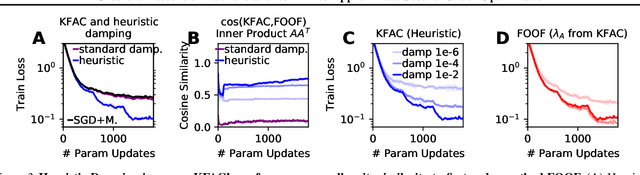
Second-order optimizers are thought to hold the potential to speed up neural network training, but due to the enormous size of the curvature matrix, they typically require approximations to be computationally tractable. The most successful family of approximations are Kronecker-Factored, block-diagonal curvature estimates (KFAC). Here, we combine tools from prior work to evaluate exact second-order updates with careful ablations to establish a surprising result: Due to its approximations, KFAC is not closely related to second-order updates, and in particular, it significantly outperforms true second-order updates. This challenges widely held believes and immediately raises the question why KFAC performs so well. We answer this question by showing that KFAC approximates a first-order algorithm, which performs gradient descent on neurons rather than weights. Finally, we show that this optimizer often improves over KFAC in terms of computational cost and data-efficiency.

Understanding Regularisation Methods for Continual Learning

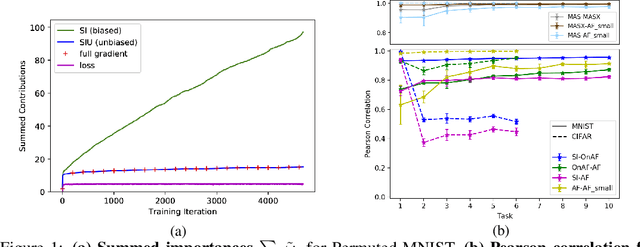
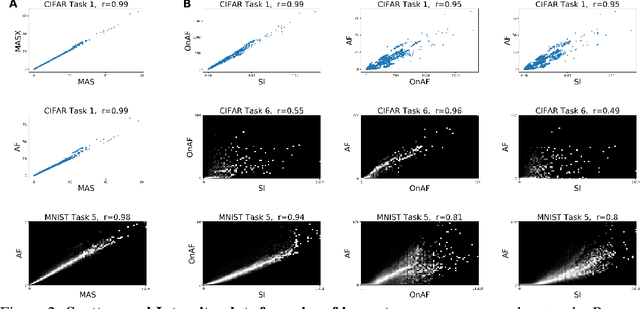
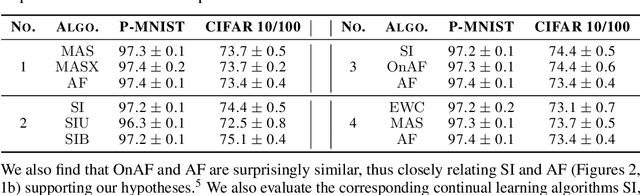
The problem of Catastrophic Forgetting has received a lot of attention in the past years. An important class of proposed solutions are so-called regularisation approaches, which protect weights from large changes according to their importances. Various ways to measure this importance have been put forward, all stemming from different theoretical or intuitive motivations. We present mathematical and empirical evidence that two of these methods -- Synaptic Intelligence and Memory Aware Synapses -- approximate a rescaled version of the Fisher Information, a theoretically justified importance measure also used in the literature. As part of our methods, we show that the importance approximation of Synaptic Intelligence is biased and that, in fact, this bias explains its performance best. Altogether, our results offer a theoretical account for the effectiveness of different regularisation approaches and uncover similarities between the methods proposed so far.

Optimal Kronecker-Sum Approximation of Real Time Recurrent Learning

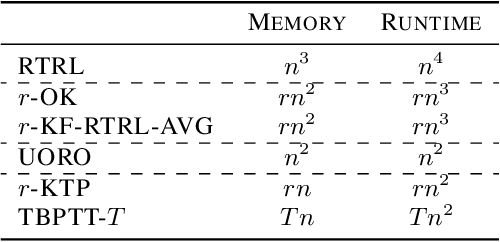
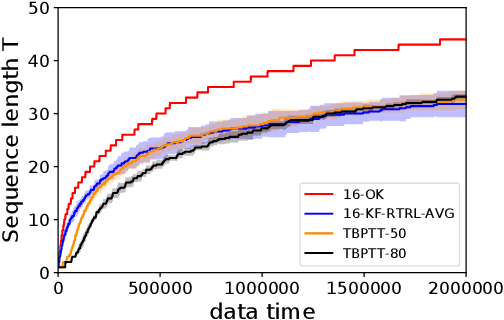
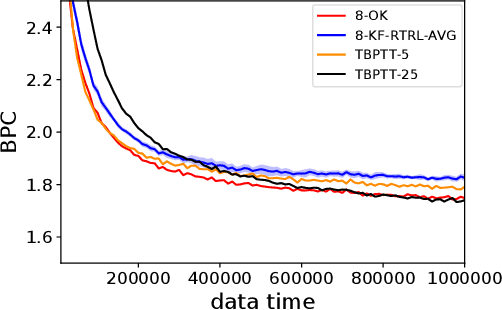
One of the central goals of Recurrent Neural Networks (RNNs) is to learn long-term dependencies in sequential data. Nevertheless, the most popular training method, Truncated Backpropagation through Time (TBPTT), categorically forbids learning dependencies beyond the truncation horizon. In contrast, the online training algorithm Real Time Recurrent Learning (RTRL) provides untruncated gradients, with the disadvantage of impractically large computational costs. Recently published approaches reduce these costs by providing noisy approximations of RTRL. We present a new approximation algorithm of RTRL, Optimal Kronecker-Sum Approximation (OK). We prove that OK is optimal for a class of approximations of RTRL, which includes all approaches published so far. Additionally, we show that OK has empirically negligible noise: Unlike previous algorithms it matches TBPTT in a real world task (character-level Penn TreeBank) and can exploit online parameter updates to outperform TBPTT in a synthetic string memorization task.