Disentangling the Predictive Variance of Deep Ensembles through the Neural Tangent Kernel
Paper and Code
Oct 18, 2022

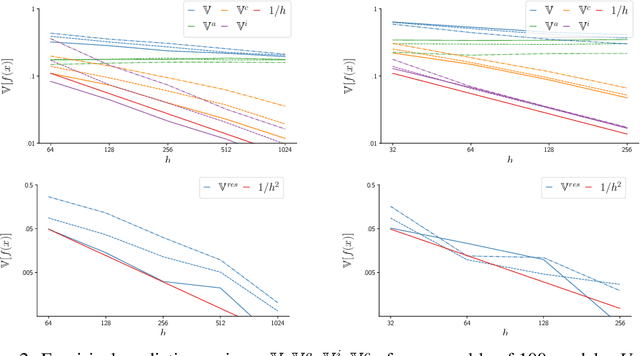
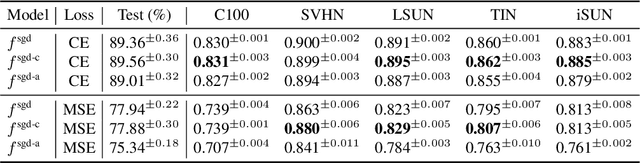
Identifying unfamiliar inputs, also known as out-of-distribution (OOD) detection, is a crucial property of any decision making process. A simple and empirically validated technique is based on deep ensembles where the variance of predictions over different neural networks acts as a substitute for input uncertainty. Nevertheless, a theoretical understanding of the inductive biases leading to the performance of deep ensemble's uncertainty estimation is missing. To improve our description of their behavior, we study deep ensembles with large layer widths operating in simplified linear training regimes, in which the functions trained with gradient descent can be described by the neural tangent kernel. We identify two sources of noise, each inducing a distinct inductive bias in the predictive variance at initialization. We further show theoretically and empirically that both noise sources affect the predictive variance of non-linear deep ensembles in toy models and realistic settings after training. Finally, we propose practical ways to eliminate part of these noise sources leading to significant changes and improved OOD detection in trained deep ensembles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge