Variance-reduced Zeroth-Order Methods for Fine-Tuning Language Models

Fine-tuning language models (LMs) has demonstrated success in a wide array of downstream tasks. However, as LMs are scaled up, the memory requirements for backpropagation become prohibitively high. Zeroth-order (ZO) optimization methods can leverage memory-efficient forward passes to estimate gradients. More recently, MeZO, an adaptation of ZO-SGD, has been shown to consistently outperform zero-shot and in-context learning when combined with suitable task prompts. In this work, we couple ZO methods with variance reduction techniques to enhance stability and convergence for inference-based LM fine-tuning. We introduce Memory-Efficient Zeroth-Order Stochastic Variance-Reduced Gradient (MeZO-SVRG) and demonstrate its efficacy across multiple LM fine-tuning tasks, eliminating the reliance on task-specific prompts. Evaluated across a range of both masked and autoregressive LMs on benchmark GLUE tasks, MeZO-SVRG outperforms MeZO with up to 20% increase in test accuracies in both full- and partial-parameter fine-tuning settings. MeZO-SVRG benefits from reduced computation time as it often surpasses MeZO's peak test accuracy with a $2\times$ reduction in GPU-hours. MeZO-SVRG significantly reduces the required memory footprint compared to first-order SGD, i.e. by $2\times$ for autoregressive models. Our experiments highlight that MeZO-SVRG's memory savings progressively improve compared to SGD with larger batch sizes.

Prominent Roles of Conditionally Invariant Components in Domain Adaptation: Theory and Algorithms

Domain adaptation (DA) is a statistical learning problem that arises when the distribution of the source data used to train a model differs from that of the target data used to evaluate the model. While many DA algorithms have demonstrated considerable empirical success, blindly applying these algorithms can often lead to worse performance on new datasets. To address this, it is crucial to clarify the assumptions under which a DA algorithm has good target performance. In this work, we focus on the assumption of the presence of conditionally invariant components (CICs), which are relevant for prediction and remain conditionally invariant across the source and target data. We demonstrate that CICs, which can be estimated through conditional invariant penalty (CIP), play three prominent roles in providing target risk guarantees in DA. First, we propose a new algorithm based on CICs, importance-weighted conditional invariant penalty (IW-CIP), which has target risk guarantees beyond simple settings such as covariate shift and label shift. Second, we show that CICs help identify large discrepancies between source and target risks of other DA algorithms. Finally, we demonstrate that incorporating CICs into the domain invariant projection (DIP) algorithm can address its failure scenario caused by label-flipping features. We support our new algorithms and theoretical findings via numerical experiments on synthetic data, MNIST, CelebA, and Camelyon17 datasets.

The Effect of SGD Batch Size on Autoencoder Learning: Sparsity, Sharpness, and Feature Learning

In this work, we investigate the dynamics of stochastic gradient descent (SGD) when training a single-neuron autoencoder with linear or ReLU activation on orthogonal data. We show that for this non-convex problem, randomly initialized SGD with a constant step size successfully finds a global minimum for any batch size choice. However, the particular global minimum found depends upon the batch size. In the full-batch setting, we show that the solution is dense (i.e., not sparse) and is highly aligned with its initialized direction, showing that relatively little feature learning occurs. On the other hand, for any batch size strictly smaller than the number of samples, SGD finds a global minimum which is sparse and nearly orthogonal to its initialization, showing that the randomness of stochastic gradients induces a qualitatively different type of "feature selection" in this setting. Moreover, if we measure the sharpness of the minimum by the trace of the Hessian, the minima found with full batch gradient descent are flatter than those found with strictly smaller batch sizes, in contrast to previous works which suggest that large batches lead to sharper minima. To prove convergence of SGD with a constant step size, we introduce a powerful tool from the theory of non-homogeneous random walks which may be of independent interest.

Interpreting and improving deep-learning models with reality checks

Recent deep-learning models have achieved impressive predictive performance by learning complex functions of many variables, often at the cost of interpretability. This chapter covers recent work aiming to interpret models by attributing importance to features and feature groups for a single prediction. Importantly, the proposed attributions assign importance to interactions between features, in addition to features in isolation. These attributions are shown to yield insights across real-world domains, including bio-imaging, cosmology image and natural-language processing. We then show how these attributions can be used to directly improve the generalization of a neural network or to distill it into a simple model. Throughout the chapter, we emphasize the use of reality checks to scrutinize the proposed interpretation techniques.

Adaptive wavelet distillation from neural networks through interpretations

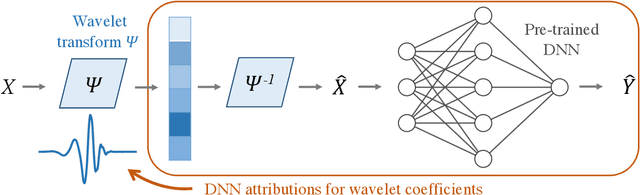
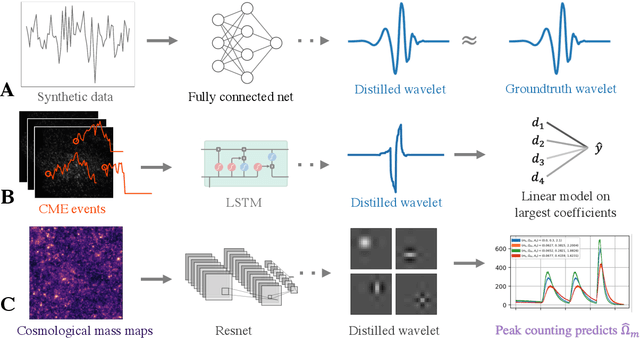
Recent deep-learning models have achieved impressive prediction performance, but often sacrifice interpretability and computational efficiency. Interpretability is crucial in many disciplines, such as science and medicine, where models must be carefully vetted or where interpretation is the goal itself. Moreover, interpretable models are concise and often yield computational efficiency. Here, we propose adaptive wavelet distillation (AWD), a method which aims to distill information from a trained neural network into a wavelet transform. Specifically, AWD penalizes feature attributions of a neural network in the wavelet domain to learn an effective multi-resolution wavelet transform. The resulting model is highly predictive, concise, computationally efficient, and has properties (such as a multi-scale structure) which make it easy to interpret. In close collaboration with domain experts, we showcase how AWD addresses challenges in two real-world settings: cosmological parameter inference and molecular-partner prediction. In both cases, AWD yields a scientifically interpretable and concise model which gives predictive performance better than state-of-the-art neural networks. Moreover, AWD identifies predictive features that are scientifically meaningful in the context of respective domains. All code and models are released in a full-fledged package available on Github (https://github.com/Yu-Group/adaptive-wavelets).

Transformation Importance with Applications to Cosmology

Machine learning lies at the heart of new possibilities for scientific discovery, knowledge generation, and artificial intelligence. Its potential benefits to these fields requires going beyond predictive accuracy and focusing on interpretability. In particular, many scientific problems require interpretations in a domain-specific interpretable feature space (e.g. the frequency domain) whereas attributions to the raw features (e.g. the pixel space) may be unintelligible or even misleading. To address this challenge, we propose TRIM (TRansformation IMportance), a novel approach which attributes importances to features in a transformed space and can be applied post-hoc to a fully trained model. TRIM is motivated by a cosmological parameter estimation problem using deep neural networks (DNNs) on simulated data, but it is generally applicable across domains/models and can be combined with any local interpretation method. In our cosmology example, combining TRIM with contextual decomposition shows promising results for identifying which frequencies a DNN uses, helping cosmologists to understand and validate that the model learns appropriate physical features rather than simulation artifacts.

Statistical guarantees for local graph clustering

Local graph clustering methods aim to find small clusters in very large graphs. These methods take as input a graph and a seed node, and they return as output a good cluster in a running time that depends on the size of the output cluster but that is independent of the size of the input graph. In this paper, we adopt a statistical perspective on local graph clustering, and we analyze the performance of the l1-regularized PageRank method (a popular local graph clustering method) for the recovery of a single target cluster, given a seed node inside the cluster. Assuming the target cluster has been generated by a random model, we present two results. In the first, we show that the optimal support of l1-regularized PageRank recovers the full target cluster, with bounded false positives. In the second, we show that if the seed node is connected solely to the target cluster then the optimal support of l1-regularized PageRank recovers exactly the target cluster. We also show that the solution path of l1-regularized PageRank is monotonic. From a computational perspective, this permits the application of the forward stagewise algorithm, which in turn permits us to approximate the entire solution path of the local cluster in a running time that does not depend on the size of the entire graph.

Alternating minimization and alternating descent over nonconvex sets

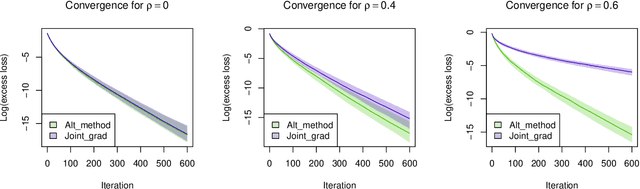
We analyze the performance of alternating minimization for loss functions optimized over two variables, where each variable may be restricted to lie in some potentially nonconvex constraint set. This type of setting arises naturally in high-dimensional statistics and signal processing, where the variables often reflect different structures or components within the signals being considered. Our analysis depends strongly on the notion of local concavity coefficients, which have been recently proposed in Barber and Ha (2017) to measure and quantify the concavity of a general nonconvex set. Our results further reveal important distinctions between alternating and non-alternating methods. Since computing the alternating minimization steps may not be tractable for some problems, we also consider an inexact version of the algorithm and provide a set of sufficient conditions to ensure fast convergence of the inexact algorithms. We demonstrate our framework on several examples, including low rank + sparse decomposition and multitask regression, and provide numerical experiments to validate our theoretical results.