Regularized Dikin Walks for Sampling Truncated Logconcave Measures, Mixed Isoperimetry and Beyond Worst-Case Analysis

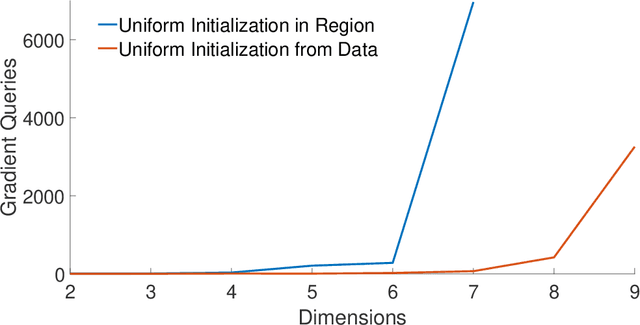
We study the problem of drawing samples from a logconcave distribution truncated on a polytope, motivated by computational challenges in Bayesian statistical models with indicator variables, such as probit regression. Building on interior point methods and the Dikin walk for sampling from uniform distributions, we analyze the mixing time of regularized Dikin walks. Our contributions are threefold. First, for a logconcave and log-smooth distribution with condition number $\kappa$, truncated on a polytope in $\mathbb{R}^n$ defined with $m$ linear constraints, we prove that the soft-threshold Dikin walk mixes in $\widetilde{O}((m+\kappa)n)$ iterations from a warm initialization. It improves upon prior work which required the polytope to be bounded and involved a bound dependent on the radius of the bounded region. Moreover, we introduce the regularized Dikin walk using Lewis weights for approximating the John ellipsoid. We show that it mixes in $\widetilde{O}((n^{2.5}+\kappa n)$. Second, we extend the mixing time guarantees mentioned above to weakly log-concave distributions truncated on polytopes, provided that they have a finite covariance matrix. Third, going beyond worst-case mixing time analysis, we demonstrate that soft-threshold Dikin walk can mix significantly faster when only a limited number of constraints intersect the high-probability mass of the distribution, improving the $\widetilde{O}((m+\kappa)n)$ upper bound to $\widetilde{O}(m + \kappa n)$. Additionally, per-iteration complexity of regularized Dikin walk and ways to generate a warm initialization are discussed to facilitate practical implementation.

PolytopeWalk: Sparse MCMC Sampling over Polytopes

High dimensional sampling is an important computational tool in statistics and other computational disciplines, with applications ranging from Bayesian statistical uncertainty quantification, metabolic modeling in systems biology to volume computation. We present $\textsf{PolytopeWalk}$, a new scalable Python library designed for uniform sampling over polytopes. The library provides an end-to-end solution, which includes preprocessing algorithms such as facial reduction and initialization methods. Six state-of-the-art MCMC algorithms on polytopes are implemented, including the Dikin, Vaidya, and John Walk. Additionally, we introduce novel sparse constrained formulations of these algorithms, enabling efficient sampling from sparse polytopes of the form $K_2 = \{x \in \mathbb{R}^d \ | \ Ax = b, x \succeq_k 0\}$. This implementation maintains sparsity in $A$, ensuring scalability to high dimensional settings $(d > 10^5)$. We demonstrate the improved sampling efficiency and per-iteration cost on both Netlib datasets and structured polytopes. $\textsf{PolytopeWalk}$ is available at github.com/ethz-randomwalk/polytopewalk with documentation at polytopewalk.readthedocs.io .

Prominent Roles of Conditionally Invariant Components in Domain Adaptation: Theory and Algorithms

Domain adaptation (DA) is a statistical learning problem that arises when the distribution of the source data used to train a model differs from that of the target data used to evaluate the model. While many DA algorithms have demonstrated considerable empirical success, blindly applying these algorithms can often lead to worse performance on new datasets. To address this, it is crucial to clarify the assumptions under which a DA algorithm has good target performance. In this work, we focus on the assumption of the presence of conditionally invariant components (CICs), which are relevant for prediction and remain conditionally invariant across the source and target data. We demonstrate that CICs, which can be estimated through conditional invariant penalty (CIP), play three prominent roles in providing target risk guarantees in DA. First, we propose a new algorithm based on CICs, importance-weighted conditional invariant penalty (IW-CIP), which has target risk guarantees beyond simple settings such as covariate shift and label shift. Second, we show that CICs help identify large discrepancies between source and target risks of other DA algorithms. Finally, we demonstrate that incorporating CICs into the domain invariant projection (DIP) algorithm can address its failure scenario caused by label-flipping features. We support our new algorithms and theoretical findings via numerical experiments on synthetic data, MNIST, CelebA, and Camelyon17 datasets.

When does Metropolized Hamiltonian Monte Carlo provably outperform Metropolis-adjusted Langevin algorithm?

We analyze the mixing time of Metropolized Hamiltonian Monte Carlo (HMC) with the leapfrog integrator to sample from a distribution on $\mathbb{R}^d$ whose log-density is smooth, has Lipschitz Hessian in Frobenius norm and satisfies isoperimetry. We bound the gradient complexity to reach $\epsilon$ error in total variation distance from a warm start by $\tilde O(d^{1/4}\text{polylog}(1/\epsilon))$ and demonstrate the benefit of choosing the number of leapfrog steps to be larger than 1. To surpass previous analysis on Metropolis-adjusted Langevin algorithm (MALA) that has $\tilde{O}(d^{1/2}\text{polylog}(1/\epsilon))$ dimension dependency in Wu et al. (2022), we reveal a key feature in our proof that the joint distribution of the location and velocity variables of the discretization of the continuous HMC dynamics stays approximately invariant. This key feature, when shown via induction over the number of leapfrog steps, enables us to obtain estimates on moments of various quantities that appear in the acceptance rate control of Metropolized HMC. Moreover, to deal with another bottleneck on the HMC proposal distribution overlap control in the literature, we provide a new approach to upper bound the Kullback-Leibler divergence between push-forwards of the Gaussian distribution through HMC dynamics initialized at two different points. Notably, our analysis does not require log-concavity or independence of the marginals, and only relies on an isoperimetric inequality. To illustrate the applicability of our result, several examples of natural functions that fall into our framework are discussed.

A Simple Proof of the Mixing of Metropolis-Adjusted Langevin Algorithm under Smoothness and Isoperimetry

We study the mixing time of Metropolis-Adjusted Langevin algorithm (MALA) for sampling a target density on $\mathbb{R}^d$. We assume that the target density satisfies $\psi_\mu$-isoperimetry and that the operator norm and trace of its Hessian are bounded by $L$ and $\Upsilon$ respectively. Our main result establishes that, from a warm start, to achieve $\epsilon$-total variation distance to the target density, MALA mixes in $O\left(\frac{(L\Upsilon)^{\frac12}}{\psi_\mu^2} \log\left(\frac{1}{\epsilon}\right)\right)$ iterations. Notably, this result holds beyond the log-concave sampling setting and the mixing time depends on only $\Upsilon$ rather than its upper bound $L d$. In the $m$-strongly logconcave and $L$-log-smooth sampling setting, our bound recovers the previous minimax mixing bound of MALA~\cite{wu2021minimax}.

Minimax Mixing Time of the Metropolis-Adjusted Langevin Algorithm for Log-Concave Sampling

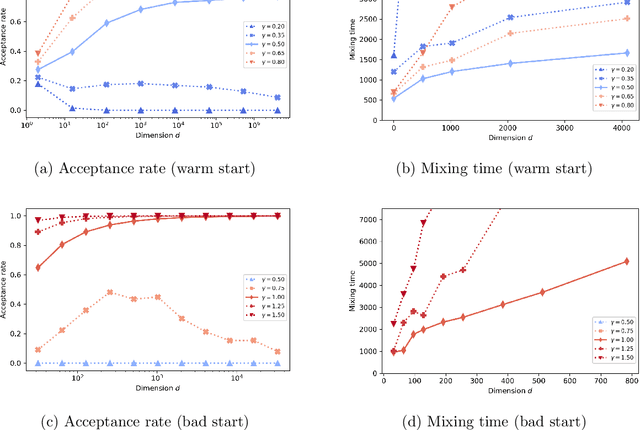
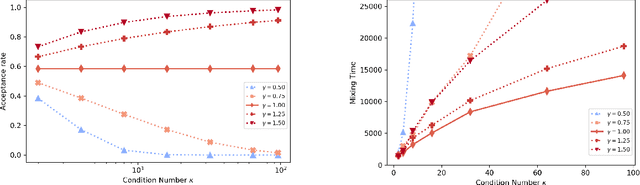
We study the mixing time of the Metropolis-adjusted Langevin algorithm (MALA) for sampling from a log-smooth and strongly log-concave distribution. We establish its optimal minimax mixing time under a warm start. Our main contribution is two-fold. First, for a $d$-dimensional log-concave density with condition number $\kappa$, we show that MALA with a warm start mixes in $\tilde O(\kappa \sqrt{d})$ iterations up to logarithmic factors. This improves upon the previous work on the dependency of either the condition number $\kappa$ or the dimension $d$. Our proof relies on comparing the leapfrog integrator with the continuous Hamiltonian dynamics, where we establish a new concentration bound for the acceptance rate. Second, we prove a spectral gap based mixing time lower bound for reversible MCMC algorithms on general state spaces. We apply this lower bound result to construct a hard distribution for which MALA requires at least $\tilde \Omega (\kappa \sqrt{d})$ steps to mix. The lower bound for MALA matches our upper bound in terms of condition number and dimension. Finally, numerical experiments are included to validate our theoretical results.

Domain adaptation under structural causal models

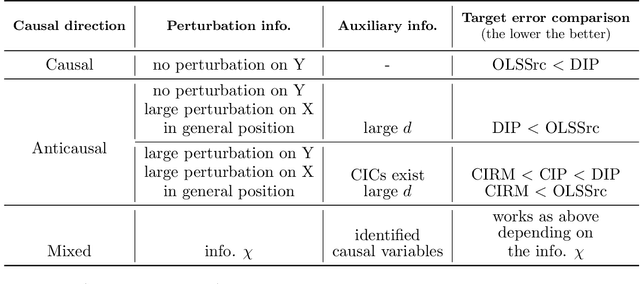
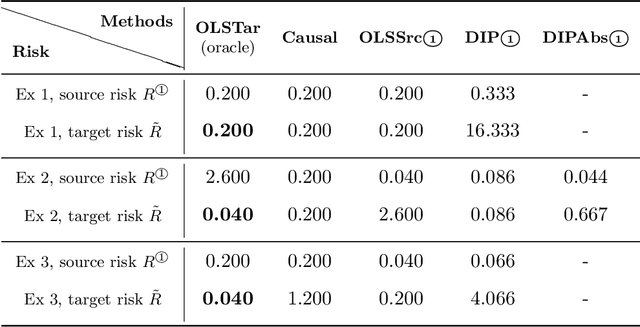
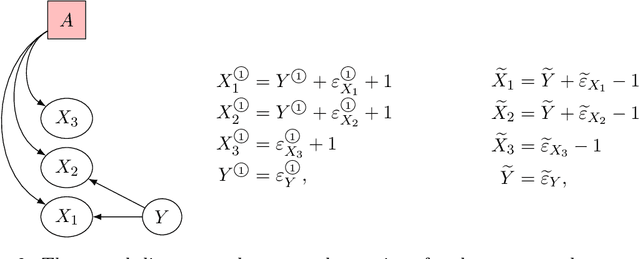
Domain adaptation (DA) arises as an important problem in statistical machine learning when the source data used to train a model is different from the target data used to test the model. Recent advances in DA have mainly been application-driven and have largely relied on the idea of a common subspace for source and target data. To understand the empirical successes and failures of DA methods, we propose a theoretical framework via structural causal models that enables analysis and comparison of the prediction performance of DA methods. This framework also allows us to itemize the assumptions needed for the DA methods to have a low target error. Additionally, with insights from our theory, we propose a new DA method called CIRM that outperforms existing DA methods when both the covariates and label distributions are perturbed in the target data. We complement the theoretical analysis with extensive simulations to show the necessity of the devised assumptions. Reproducible synthetic and real data experiments are also provided to illustrate the strengths and weaknesses of DA methods when parts of the assumptions of our theory are violated.

Fast mixing of Metropolized Hamiltonian Monte Carlo: Benefits of multi-step gradients

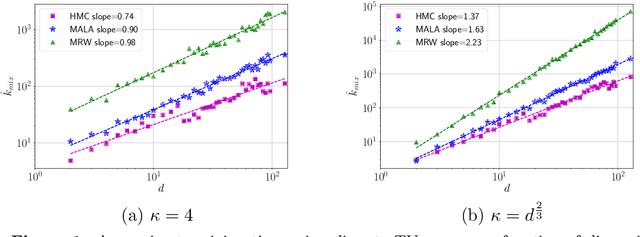
Hamiltonian Monte Carlo (HMC) is a state-of-the-art Markov chain Monte Carlo sampling algorithm for drawing samples from smooth probability densities over continuous spaces. We study the variant most widely used in practice, Metropolized HMC with the St\"{o}rmer-Verlet or leapfrog integrator, and make two primary contributions. First, we provide a non-asymptotic upper bound on the mixing time of the Metropolized HMC with explicit choices of stepsize and number of leapfrog steps. This bound gives a precise quantification of the faster convergence of Metropolized HMC relative to simpler MCMC algorithms such as the Metropolized random walk, or Metropolized Langevin algorithm. Second, we provide a general framework for sharpening mixing time bounds Markov chains initialized at a substantial distance from the target distribution over continuous spaces. We apply this sharpening device to the Metropolized random walk and Langevin algorithms, thereby obtaining improved mixing time bounds from a non-warm initial distribution.

Sampling Can Be Faster Than Optimization

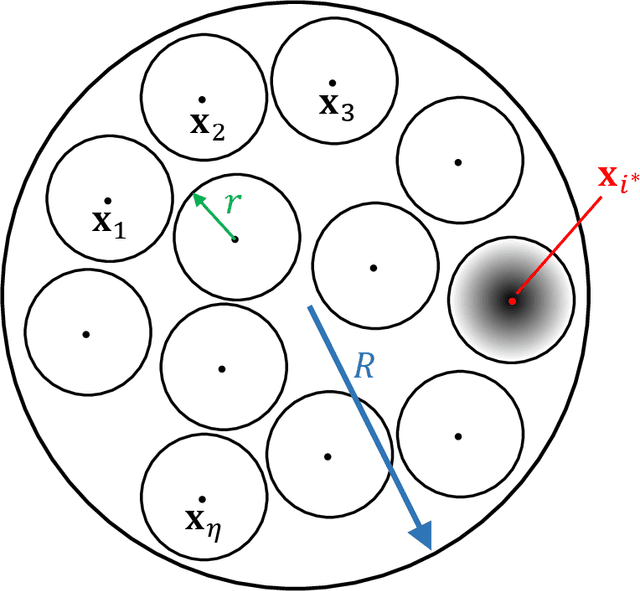
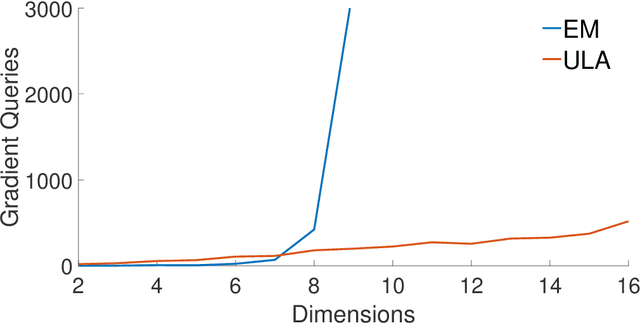
Optimization algorithms and Monte Carlo sampling algorithms have provided the computational foundations for the rapid growth in applications of statistical machine learning in recent years. There is, however, limited theoretical understanding of the relationships between these two kinds of methodology, and limited understanding of relative strengths and weaknesses. Moreover, existing results have been obtained primarily in the setting of convex functions (for optimization) and log-concave functions (for sampling). In this setting, where local properties determine global properties, optimization algorithms are unsurprisingly more efficient computationally than sampling algorithms. We instead examine a class of nonconvex objective functions that arise in mixture modeling and multi-stable systems. In this nonconvex setting, we find that the computational complexity of sampling algorithms scales linearly with the model dimension while that of optimization algorithms scales exponentially.

Fast MCMC sampling algorithms on polytopes

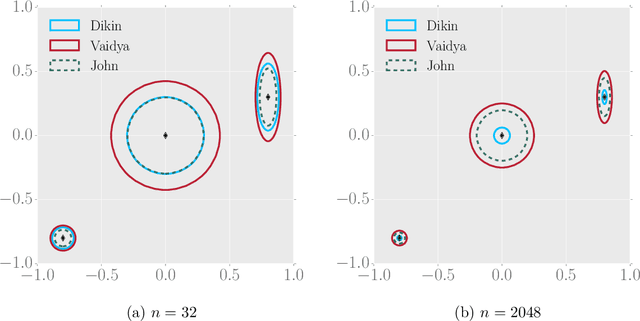
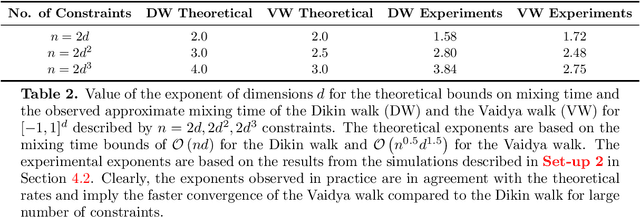
We propose and analyze two new MCMC sampling algorithms, the Vaidya walk and the John walk, for generating samples from the uniform distribution over a polytope. Both random walks are sampling algorithms derived from interior point methods. The former is based on volumetric-logarithmic barrier introduced by Vaidya whereas the latter uses John's ellipsoids. We show that the Vaidya walk mixes in significantly fewer steps than the logarithmic-barrier based Dikin walk studied in past work. For a polytope in $\mathbb{R}^d$ defined by $n >d$ linear constraints, we show that the mixing time from a warm start is bounded as $\mathcal{O}(n^{0.5}d^{1.5})$, compared to the $\mathcal{O}(nd)$ mixing time bound for the Dikin walk. The cost of each step of the Vaidya walk is of the same order as the Dikin walk, and at most twice as large in terms of constant pre-factors. For the John walk, we prove an $\mathcal{O}(d^{2.5}\cdot\log^4(n/d))$ bound on its mixing time and conjecture that an improved variant of it could achieve a mixing time of $\mathcal{O}(d^2\cdot\text{polylog}(n/d))$. Additionally, we propose variants of the Vaidya and John walks that mix in polynomial time from a deterministic starting point. We illustrate the speed-up of the Vaidya walk over the Dikin walk via several numerical examples.