Prominent Roles of Conditionally Invariant Components in Domain Adaptation: Theory and Algorithms

Domain adaptation (DA) is a statistical learning problem that arises when the distribution of the source data used to train a model differs from that of the target data used to evaluate the model. While many DA algorithms have demonstrated considerable empirical success, blindly applying these algorithms can often lead to worse performance on new datasets. To address this, it is crucial to clarify the assumptions under which a DA algorithm has good target performance. In this work, we focus on the assumption of the presence of conditionally invariant components (CICs), which are relevant for prediction and remain conditionally invariant across the source and target data. We demonstrate that CICs, which can be estimated through conditional invariant penalty (CIP), play three prominent roles in providing target risk guarantees in DA. First, we propose a new algorithm based on CICs, importance-weighted conditional invariant penalty (IW-CIP), which has target risk guarantees beyond simple settings such as covariate shift and label shift. Second, we show that CICs help identify large discrepancies between source and target risks of other DA algorithms. Finally, we demonstrate that incorporating CICs into the domain invariant projection (DIP) algorithm can address its failure scenario caused by label-flipping features. We support our new algorithms and theoretical findings via numerical experiments on synthetic data, MNIST, CelebA, and Camelyon17 datasets.

Minimax Mixing Time of the Metropolis-Adjusted Langevin Algorithm for Log-Concave Sampling

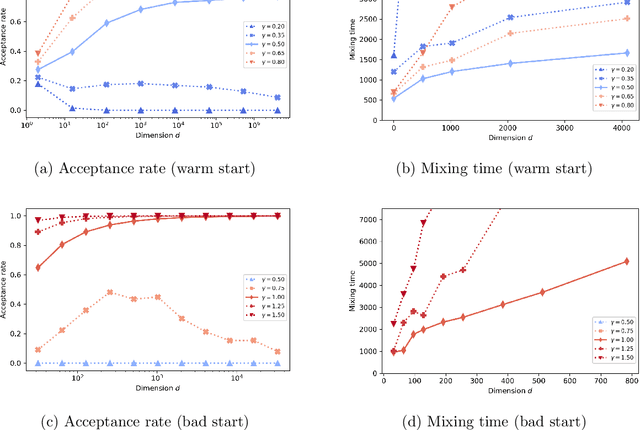
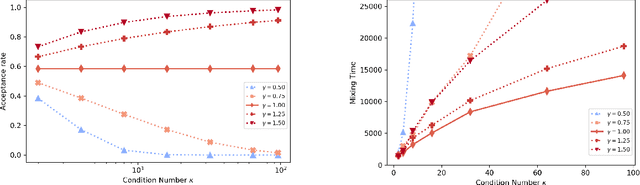
We study the mixing time of the Metropolis-adjusted Langevin algorithm (MALA) for sampling from a log-smooth and strongly log-concave distribution. We establish its optimal minimax mixing time under a warm start. Our main contribution is two-fold. First, for a $d$-dimensional log-concave density with condition number $\kappa$, we show that MALA with a warm start mixes in $\tilde O(\kappa \sqrt{d})$ iterations up to logarithmic factors. This improves upon the previous work on the dependency of either the condition number $\kappa$ or the dimension $d$. Our proof relies on comparing the leapfrog integrator with the continuous Hamiltonian dynamics, where we establish a new concentration bound for the acceptance rate. Second, we prove a spectral gap based mixing time lower bound for reversible MCMC algorithms on general state spaces. We apply this lower bound result to construct a hard distribution for which MALA requires at least $\tilde \Omega (\kappa \sqrt{d})$ steps to mix. The lower bound for MALA matches our upper bound in terms of condition number and dimension. Finally, numerical experiments are included to validate our theoretical results.