Scott Schmidler
Minimax Mixing Time of the Metropolis-Adjusted Langevin Algorithm for Log-Concave Sampling
Sep 27, 2021
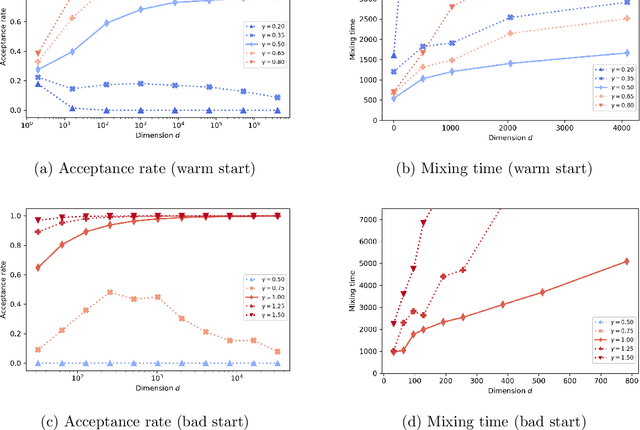
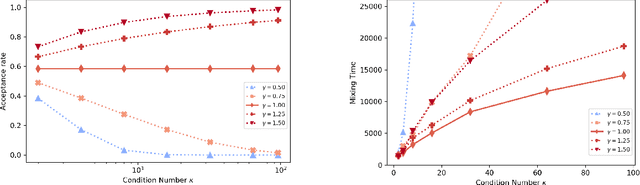
Abstract:We study the mixing time of the Metropolis-adjusted Langevin algorithm (MALA) for sampling from a log-smooth and strongly log-concave distribution. We establish its optimal minimax mixing time under a warm start. Our main contribution is two-fold. First, for a $d$-dimensional log-concave density with condition number $\kappa$, we show that MALA with a warm start mixes in $\tilde O(\kappa \sqrt{d})$ iterations up to logarithmic factors. This improves upon the previous work on the dependency of either the condition number $\kappa$ or the dimension $d$. Our proof relies on comparing the leapfrog integrator with the continuous Hamiltonian dynamics, where we establish a new concentration bound for the acceptance rate. Second, we prove a spectral gap based mixing time lower bound for reversible MCMC algorithms on general state spaces. We apply this lower bound result to construct a hard distribution for which MALA requires at least $\tilde \Omega (\kappa \sqrt{d})$ steps to mix. The lower bound for MALA matches our upper bound in terms of condition number and dimension. Finally, numerical experiments are included to validate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge