Initialization Matters: On the Benign Overfitting of Two-Layer ReLU CNN with Fully Trainable Layers

Benign overfitting refers to how over-parameterized neural networks can fit training data perfectly and generalize well to unseen data. While this has been widely investigated theoretically, existing works are limited to two-layer networks with fixed output layers, where only the hidden weights are trained. We extend the analysis to two-layer ReLU convolutional neural networks (CNNs) with fully trainable layers, which is closer to the practice. Our results show that the initialization scaling of the output layer is crucial to the training dynamics: large scales make the model training behave similarly to that with the fixed output, the hidden layer grows rapidly while the output layer remains largely unchanged; in contrast, small scales result in more complex layer interactions, the hidden layer initially grows to a specific ratio relative to the output layer, after which both layers jointly grow and maintain that ratio throughout training. Furthermore, in both settings, we provide nearly matching upper and lower bounds on the test errors, identifying the sharp conditions on the initialization scaling and signal-to-noise ratio (SNR) in which the benign overfitting can be achieved or not. Numerical experiments back up the theoretical results.

Benign Overfitting in Single-Head Attention

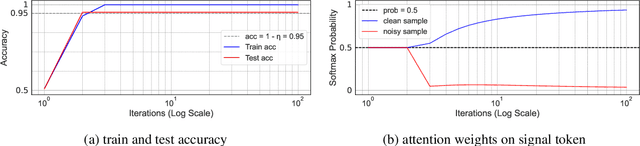
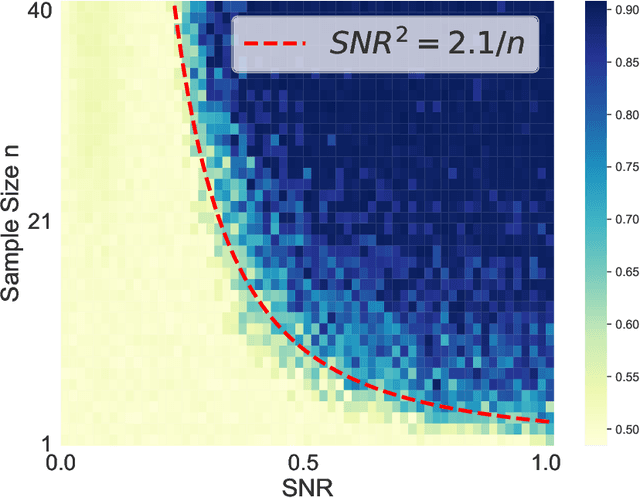
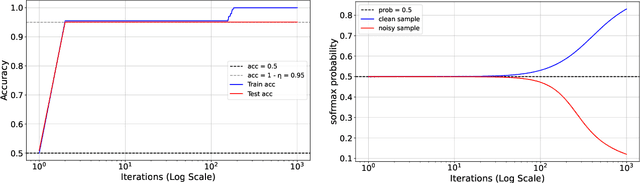
The phenomenon of benign overfitting, where a trained neural network perfectly fits noisy training data but still achieves near-optimal test performance, has been extensively studied in recent years for linear models and fully-connected/convolutional networks. In this work, we study benign overfitting in a single-head softmax attention model, which is the fundamental building block of Transformers. We prove that under appropriate conditions, the model exhibits benign overfitting in a classification setting already after two steps of gradient descent. Moreover, we show conditions where a minimum-norm/maximum-margin interpolator exhibits benign overfitting. We study how the overfitting behavior depends on the signal-to-noise ratio (SNR) of the data distribution, namely, the ratio between norms of signal and noise tokens, and prove that a sufficiently large SNR is both necessary and sufficient for benign overfitting.