A. Michael Carrell
Attribute Diversity Determines the Systematicity Gap in VQA
Nov 15, 2023



Abstract:The degree to which neural networks can generalize to new combinations of familiar concepts, and the conditions under which they are able to do so, has long been an open question. In this work, we study the systematicity gap in visual question answering: the performance difference between reasoning on previously seen and unseen combinations of object attributes. To test, we introduce a novel diagnostic dataset, CLEVR-HOPE. We find that while increased quantity of training data does not reduce the systematicity gap, increased training data diversity of the attributes in the unseen combination does. In all, our experiments suggest that the more distinct attribute type combinations are seen during training, the more systematic we can expect the resulting model to be.
The Calibration Generalization Gap
Oct 06, 2022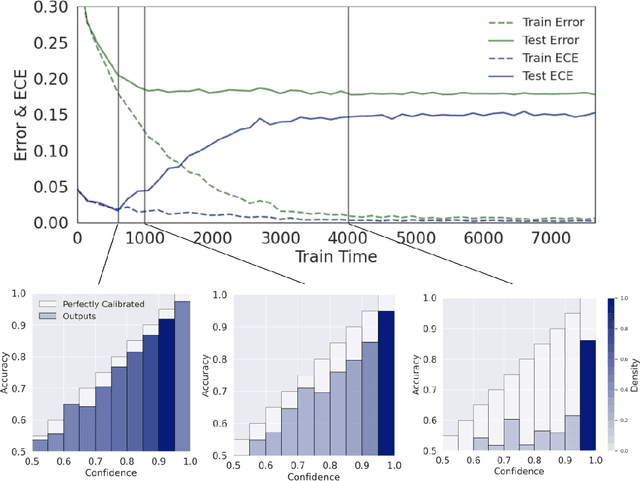
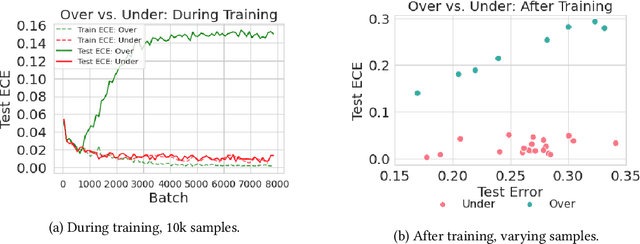
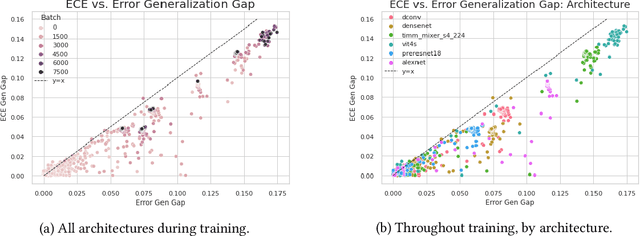
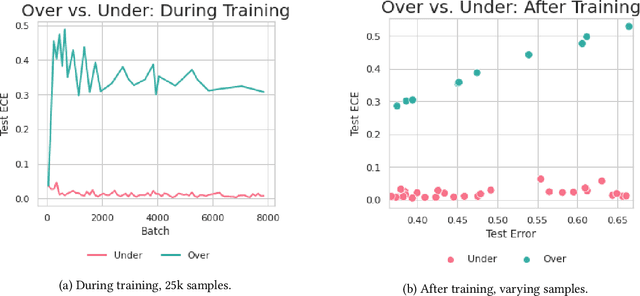
Abstract:Calibration is a fundamental property of a good predictive model: it requires that the model predicts correctly in proportion to its confidence. Modern neural networks, however, provide no strong guarantees on their calibration -- and can be either poorly calibrated or well-calibrated depending on the setting. It is currently unclear which factors contribute to good calibration (architecture, data augmentation, overparameterization, etc), though various claims exist in the literature. We propose a systematic way to study the calibration error: by decomposing it into (1) calibration error on the train set, and (2) the calibration generalization gap. This mirrors the fundamental decomposition of generalization. We then investigate each of these terms, and give empirical evidence that (1) DNNs are typically always calibrated on their train set, and (2) the calibration generalization gap is upper-bounded by the standard generalization gap. Taken together, this implies that models with small generalization gap (|Test Error - Train Error|) are well-calibrated. This perspective unifies many results in the literature, and suggests that interventions which reduce the generalization gap (such as adding data, using heavy augmentation, or smaller model size) also improve calibration. We thus hope our initial study lays the groundwork for a more systematic and comprehensive understanding of the relation between calibration, generalization, and optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge