Robust and Resource Efficient Identification of Two Hidden Layer Neural Networks
Paper and Code
Jun 30, 2019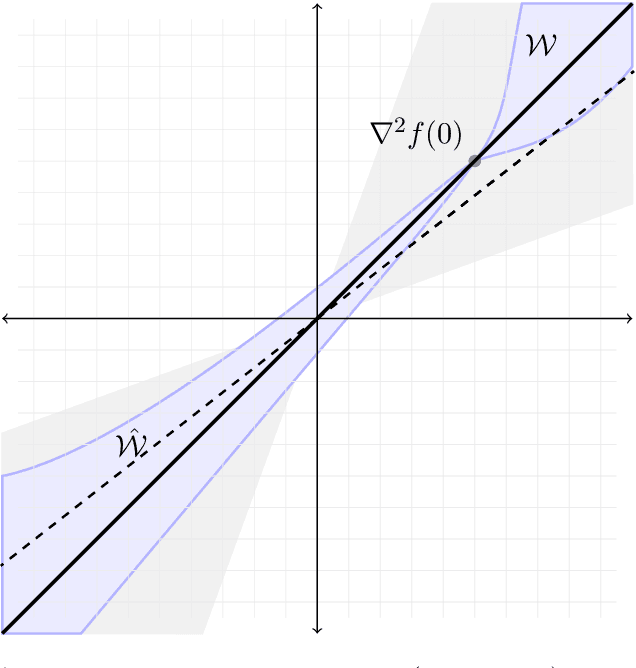
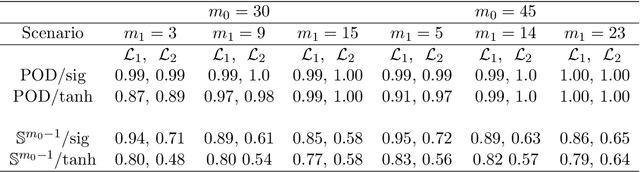
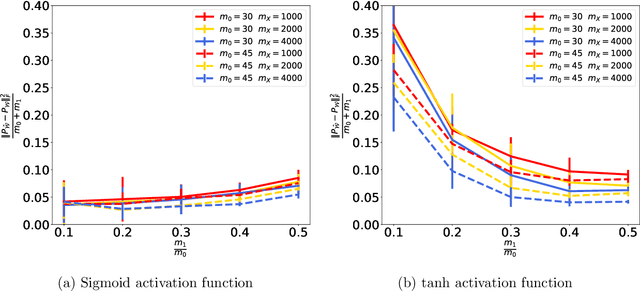
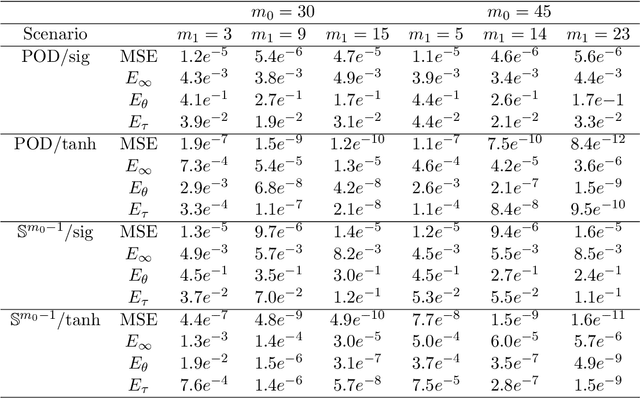
We address the structure identification and the uniform approximation of two fully nonlinear layer neural networks of the type $f(x)=1^T h(B^T g(A^T x))$ on $\mathbb R^d$ from a small number of query samples. We approach the problem by sampling actively finite difference approximations to Hessians of the network. Gathering several approximate Hessians allows reliably to approximate the matrix subspace $\mathcal W$ spanned by symmetric tensors $a_1 \otimes a_1 ,\dots,a_{m_0}\otimes a_{m_0}$ formed by weights of the first layer together with the entangled symmetric tensors $v_1 \otimes v_1 ,\dots,v_{m_1}\otimes v_{m_1}$, formed by suitable combinations of the weights of the first and second layer as $v_\ell=A G_0 b_\ell/\|A G_0 b_\ell\|_2$, $\ell \in [m_1]$, for a diagonal matrix $G_0$ depending on the activation functions of the first layer. The identification of the 1-rank symmetric tensors within $\mathcal W$ is then performed by the solution of a robust nonlinear program. We provide guarantees of stable recovery under a posteriori verifiable conditions. We further address the correct attribution of approximate weights to the first or second layer. By using a suitably adapted gradient descent iteration, it is possible then to estimate, up to intrinsic symmetries, the shifts of the activations functions of the first layer and compute exactly the matrix $G_0$. Our method of identification of the weights of the network is fully constructive, with quantifiable sample complexity, and therefore contributes to dwindle the black-box nature of the network training phase. We corroborate our theoretical results by extensive numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge