Convolutional Neural Networks as 2-D systems

This paper introduces a novel representation of convolutional Neural Networks (CNNs) in terms of 2-D dynamical systems. To this end, the usual description of convolutional layers with convolution kernels, i.e., the impulse responses of linear filters, is realized in state space as a linear time-invariant 2-D system. The overall convolutional Neural Network composed of convolutional layers and nonlinear activation functions is then viewed as a 2-D version of a Lur'e system, i.e., a linear dynamical system interconnected with static nonlinear components. One benefit of this 2-D Lur'e system perspective on CNNs is that we can use robust control theory much more efficiently for Lipschitz constant estimation than previously possible.

Learning-enhanced robust controller synthesis with rigorous statistical and control-theoretic guarantees

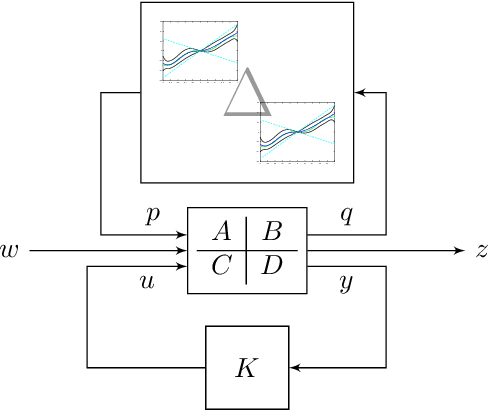
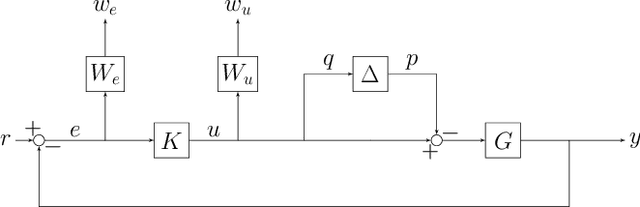
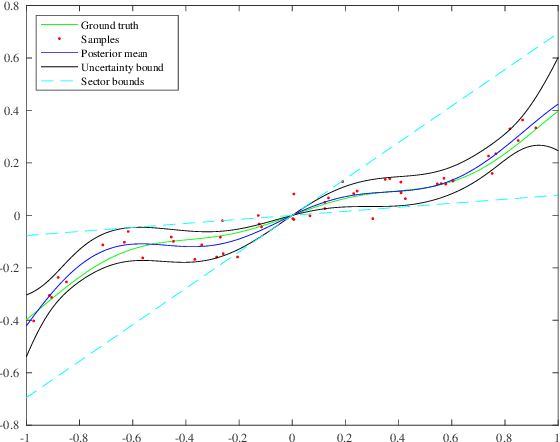
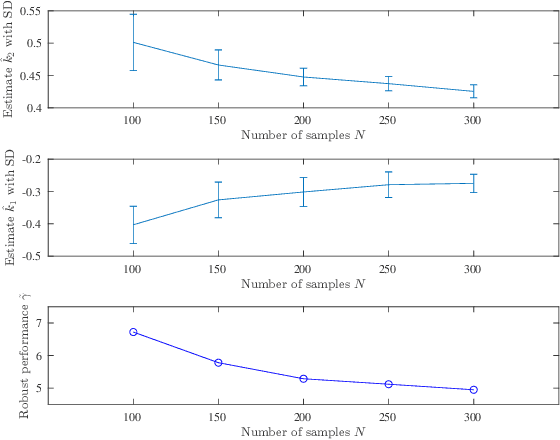
The combination of machine learning with control offers many opportunities, in particular for robust control. However, due to strong safety and reliability requirements in many real-world applications, providing rigorous statistical and control-theoretic guarantees is of utmost importance, yet difficult to achieve for learning-based control schemes. We present a general framework for learning-enhanced robust control that allows for systematic integration of prior engineering knowledge, is fully compatible with modern robust control and still comes with rigorous and practically meaningful guarantees. Building on the established Linear Fractional Representation and Integral Quadratic Constraints framework, we integrate Gaussian Process Regression as a learning component and state-of-the-art robust controller synthesis. In a concrete robust control example, our approach is demonstrated to yield improved performance with more data, while guarantees are maintained throughout.

Practical and Rigorous Uncertainty Bounds for Gaussian Process Regression

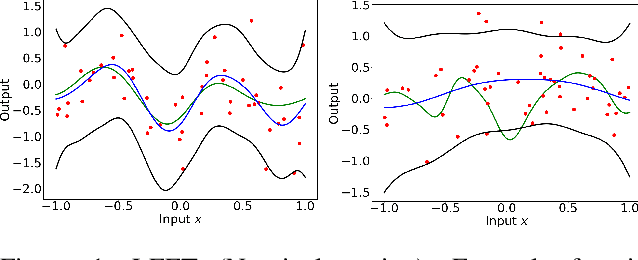
Gaussian Process Regression is a popular nonparametric regression method based on Bayesian principles that provides uncertainty estimates for its predictions. However, these estimates are of a Bayesian nature, whereas for some important applications, like learning-based control with safety guarantees, frequentist uncertainty bounds are required. Although such rigorous bounds are available for Gaussian Processes, they are too conservative to be useful in applications. This often leads practitioners to replacing these bounds by heuristics, thus breaking all theoretical guarantees. To address this problem, we introduce new uncertainty bounds that are rigorous, yet practically useful at the same time. In particular, the bounds can be explicitly evaluated and are much less conservative than state of the art results. Furthermore, we show that certain model misspecifications lead to only graceful degradation. We demonstrate these advantages and the usefulness of our results for learning-based control with numerical examples.