Identification of Shallow Neural Networks by Fewest Samples

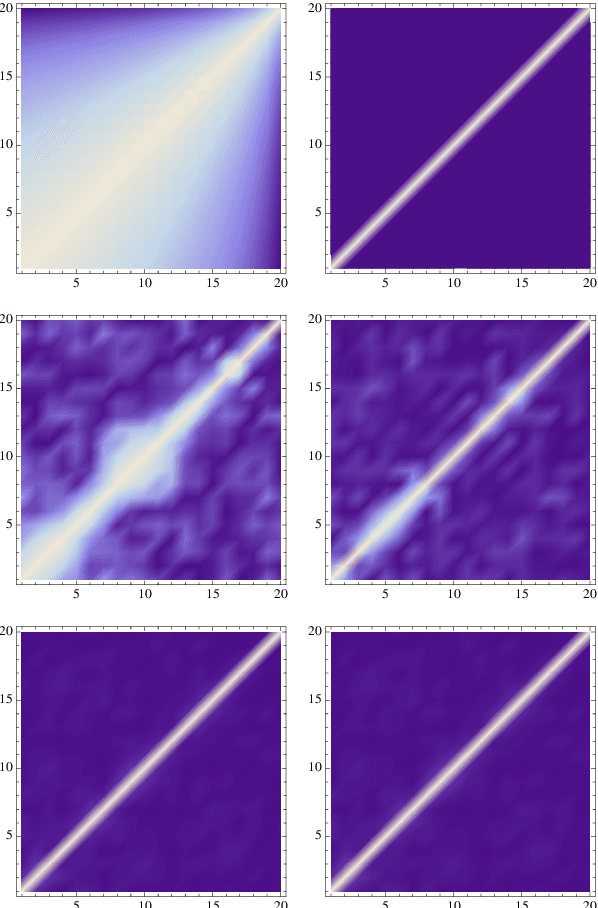
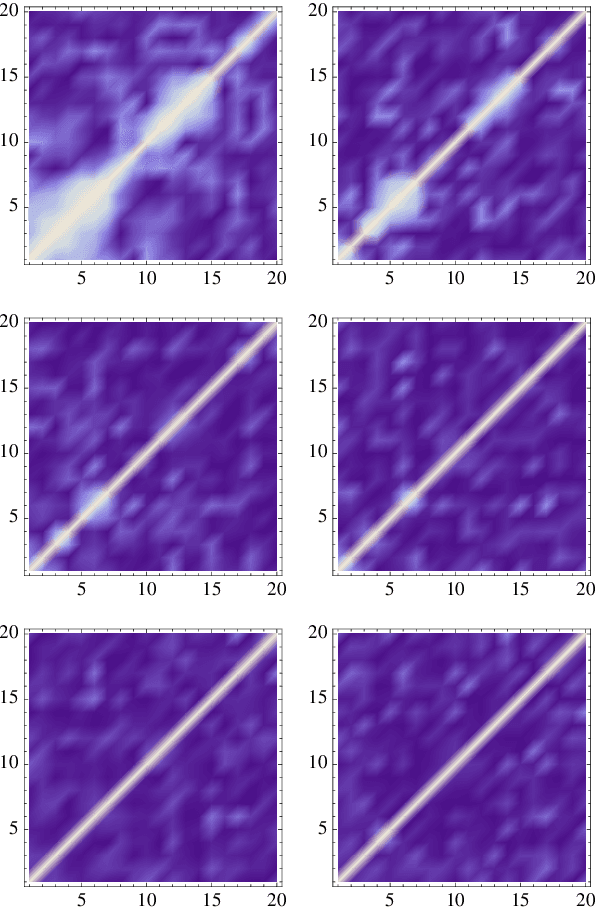
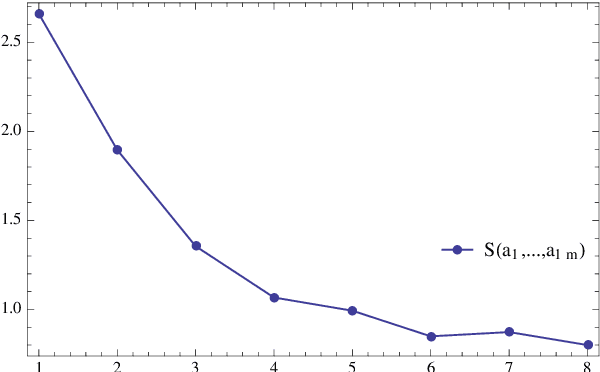
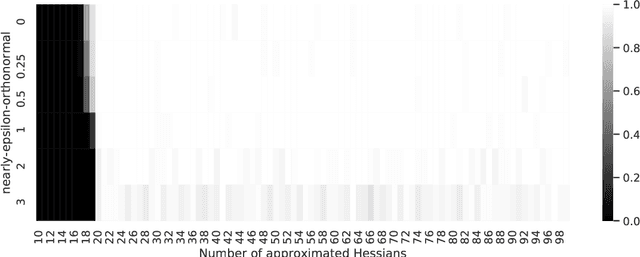
We address the uniform approximation of sums of ridge functions $\sum_{i=1}^m g_i(a_i\cdot x)$ on ${\mathbb R}^d$, representing the shallowest form of feed-forward neural network, from a small number of query samples, under mild smoothness assumptions on the functions $g_i$'s and near-orthogonality of the ridge directions $a_i$'s. The sample points are randomly generated and are universal, in the sense that the sampled queries on those points will allow the proposed recovery algorithms to perform a uniform approximation of any sum of ridge functions with high-probability. Our general approximation strategy is developed as a sequence of algorithms to perform individual sub-tasks. We first approximate the span of the ridge directions. Then we use a straightforward substitution, which reduces the dimensionality of the problem from $d$ to $m$. The core of the construction is then the approximation of ridge directions expressed in terms of rank-$1$ matrices $a_i \otimes a_i$, realized by formulating their individual identification as a suitable nonlinear program, maximizing the spectral norm of certain competitors constrained over the unit Frobenius sphere. The final step is then to approximate the functions $g_1,\dots,g_m$ by $\hat g_1,\dots,\hat g_m$. Higher order differentiation, as used in our construction, of sums of ridge functions or of their compositions, as in deeper neural network, yields a natural connection between neural network weight identification and tensor product decomposition identification. In the case of the shallowest feed-forward neural network, we show that second order differentiation and tensors of order two (i.e., matrices) suffice.

Non-asymptotic Analysis of $\ell_1$-norm Support Vector Machines

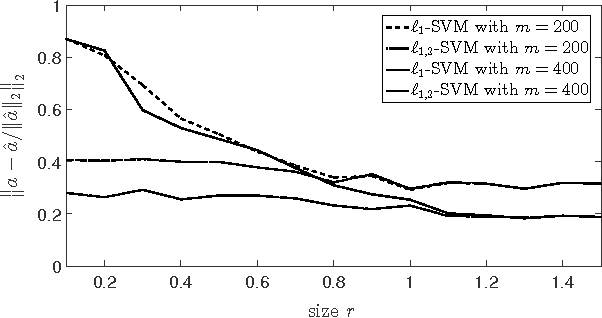
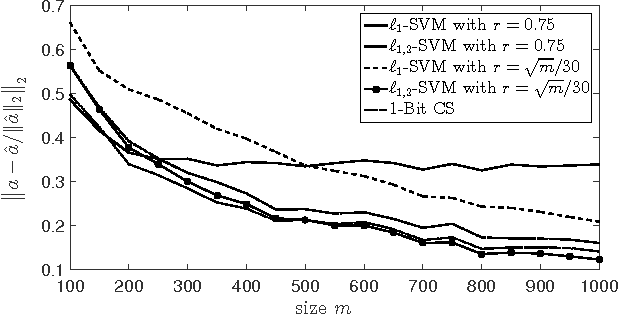
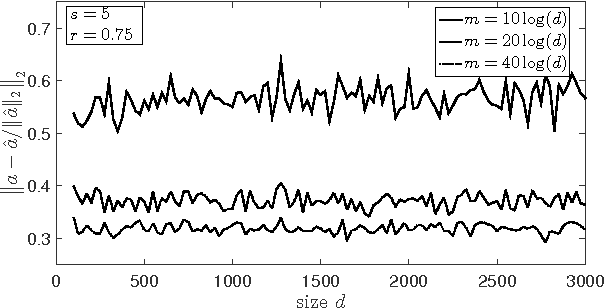
Support Vector Machines (SVM) with $\ell_1$ penalty became a standard tool in analysis of highdimensional classification problems with sparsity constraints in many applications including bioinformatics and signal processing. Although SVM have been studied intensively in the literature, this paper has to our knowledge first non-asymptotic results on the performance of $\ell_1$-SVM in identification of sparse classifiers. We show that a $d$-dimensional $s$-sparse classification vector can be (with high probability) well approximated from only $O(s\log(d))$ Gaussian trials. The methods used in the proof include concentration of measure and probability in Banach spaces.