Non-asymptotic Analysis of $\ell_1$-norm Support Vector Machines
Paper and Code
Sep 27, 2015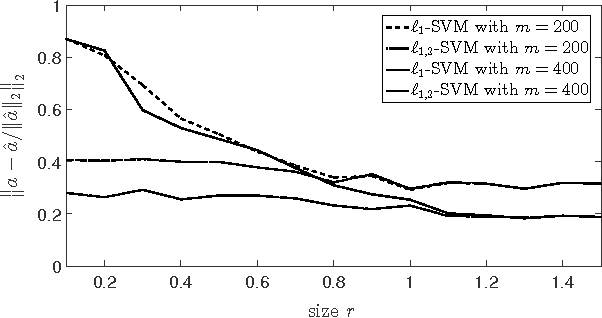
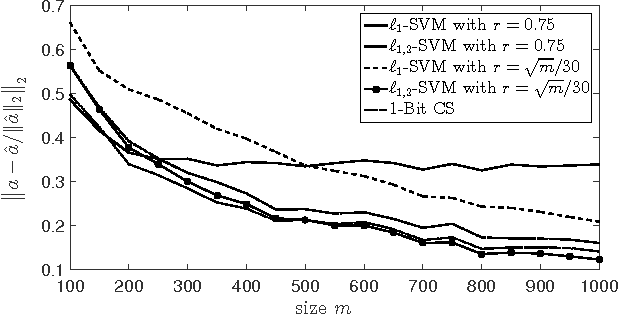
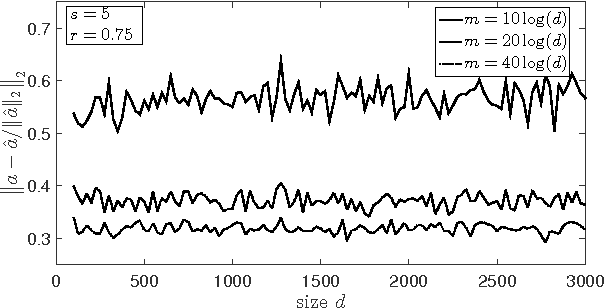
Support Vector Machines (SVM) with $\ell_1$ penalty became a standard tool in analysis of highdimensional classification problems with sparsity constraints in many applications including bioinformatics and signal processing. Although SVM have been studied intensively in the literature, this paper has to our knowledge first non-asymptotic results on the performance of $\ell_1$-SVM in identification of sparse classifiers. We show that a $d$-dimensional $s$-sparse classification vector can be (with high probability) well approximated from only $O(s\log(d))$ Gaussian trials. The methods used in the proof include concentration of measure and probability in Banach spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge