A Continuous-time Stochastic Gradient Descent Method for Continuous Data
Paper and Code
Dec 07, 2021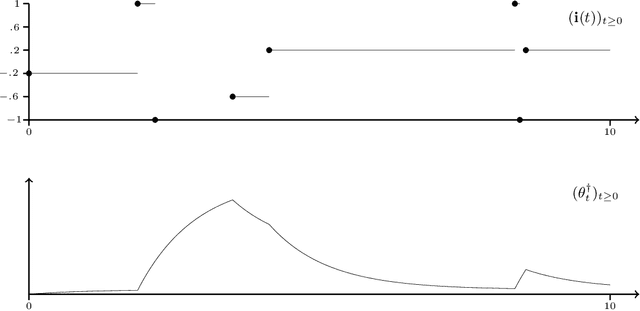
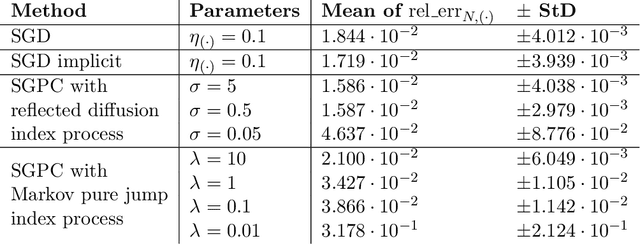
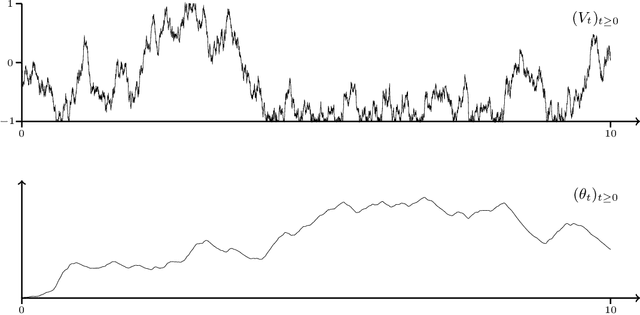
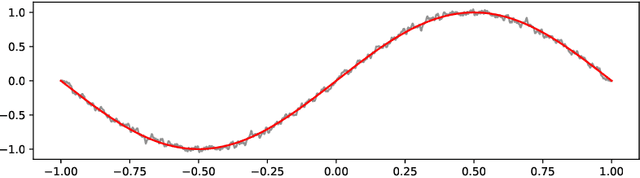
Optimization problems with continuous data appear in, e.g., robust machine learning, functional data analysis, and variational inference. Here, the target function is given as an integral over a family of (continuously) indexed target functions - integrated with respect to a probability measure. Such problems can often be solved by stochastic optimization methods: performing optimization steps with respect to the indexed target function with randomly switched indices. In this work, we study a continuous-time variant of the stochastic gradient descent algorithm for optimization problems with continuous data. This so-called stochastic gradient process consists in a gradient flow minimizing an indexed target function that is coupled with a continuous-time index process determining the index. Index processes are, e.g., reflected diffusions, pure jump processes, or other L\'evy processes on compact spaces. Thus, we study multiple sampling patterns for the continuous data space and allow for data simulated or streamed at runtime of the algorithm. We analyze the approximation properties of the stochastic gradient process and study its longtime behavior and ergodicity under constant and decreasing learning rates. We end with illustrating the applicability of the stochastic gradient process in a polynomial regression problem with noisy functional data, as well as in a physics-informed neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge