Analysis of Stochastic Gradient Descent in Continuous Time

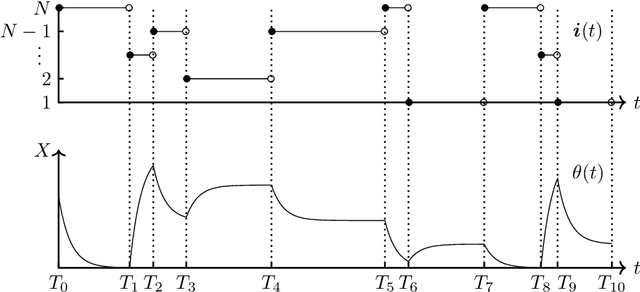
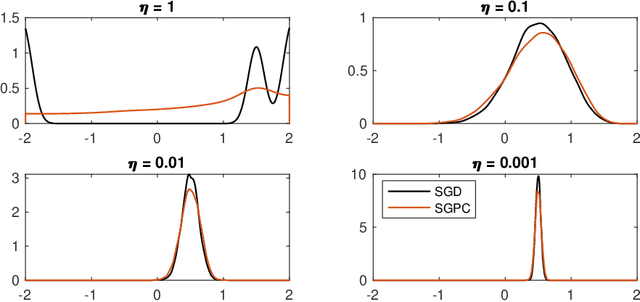
We introduce the stochastic gradient process as a continuous-time representation of the celebrated stochastic gradient descent algorithm. The stochastic gradient process is a dynamical system that is coupled with a continuous-time Markov process living on a finite state space. The dynamical system - a gradient flow - represents the gradient descent part, the process on the finite state space represents the stochastic switching among the data sets. Processes of this type are, for instance, used to model clonal populations in fluctuating environments. After introducing it, we study theoretical properties of the stochastic gradient process. We show that it converges weakly to the gradient flow with respect to the full target function, as the learning rate approaches zero. Moreover, we give assumptions under which the stochastic gradient process is exponentially ergodic. We then additionally assume that the single target functions are strongly convex and the learning rate goes to zero sufficiently slowly. In this case, the process converges weakly at exponential rate to any neighbourhood of the global minimum of the full target function. We conclude with a discussion of discretisation strategies for the stochastic gradient process and illustrate our concepts in numerical experiments.