Hidden Knowledge: Mathematical Methods for the Extraction of the Fingerprint of Medieval Paper from Digital Images

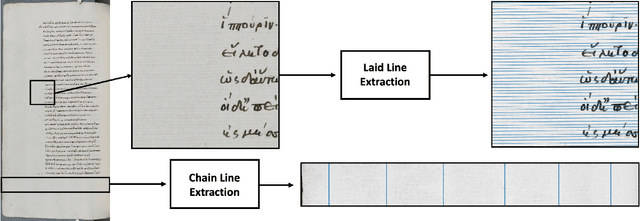
Medieval paper, a handmade product, is made with a mould which leaves an indelible imprint on the sheet of paper. This imprint includes chain lines, laid lines and watermarks which are often visible on the sheet. Extracting these features allows the identification of paper stock and gives information about chronology, localisation and movement of books and people. Most computational work for feature extraction of paper analysis has so far focused on radiography or transmitted light images. While these imaging methods provide clear visualisation for the features of interest, they are expensive and time consuming in their acquisition and not feasible for smaller institutions. However, reflected light images of medieval paper manuscripts are abundant and possibly cheaper in their acquisition. In this paper, we propose algorithms to detect and extract the laid and chain lines from reflected light images. We tackle the main drawback of reflected light images, that is, the low contrast attenuation of lines and intensity jumps due to noise and degradation, by employing the spectral total variation decomposition and develop methods for subsequent line extraction. Our results clearly demonstrate the feasibility of using reflected light images in paper analysis. This work enables the feature extraction for paper manuscripts that have otherwise not been analysed due to a lack of appropriate images. We also open the door for paper stock identification at scale.

Can Physics-Informed Neural Networks beat the Finite Element Method?

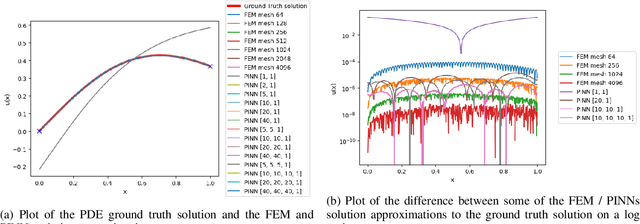
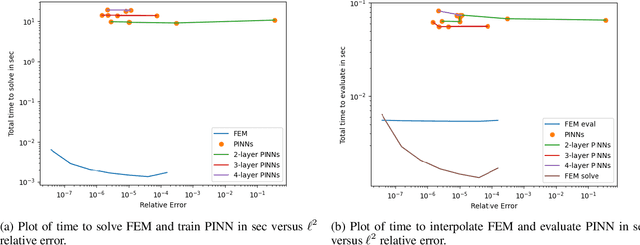
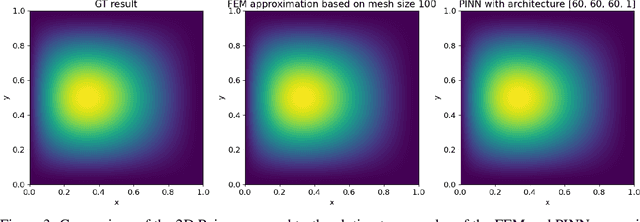
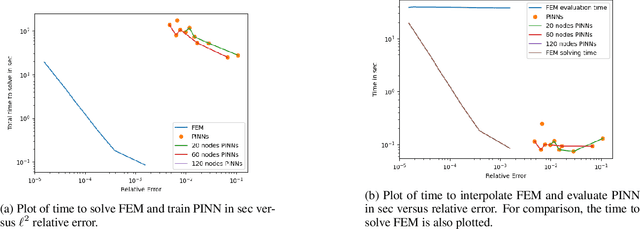
Partial differential equations play a fundamental role in the mathematical modelling of many processes and systems in physical, biological and other sciences. To simulate such processes and systems, the solutions of PDEs often need to be approximated numerically. The finite element method, for instance, is a usual standard methodology to do so. The recent success of deep neural networks at various approximation tasks has motivated their use in the numerical solution of PDEs. These so-called physics-informed neural networks and their variants have shown to be able to successfully approximate a large range of partial differential equations. So far, physics-informed neural networks and the finite element method have mainly been studied in isolation of each other. In this work, we compare the methodologies in a systematic computational study. Indeed, we employ both methods to numerically solve various linear and nonlinear partial differential equations: Poisson in 1D, 2D, and 3D, Allen-Cahn in 1D, semilinear Schr\"odinger in 1D and 2D. We then compare computational costs and approximation accuracies. In terms of solution time and accuracy, physics-informed neural networks have not been able to outperform the finite element method in our study. In some experiments, they were faster at evaluating the solved PDE.

Unsupervised Learning of the Total Variation Flow

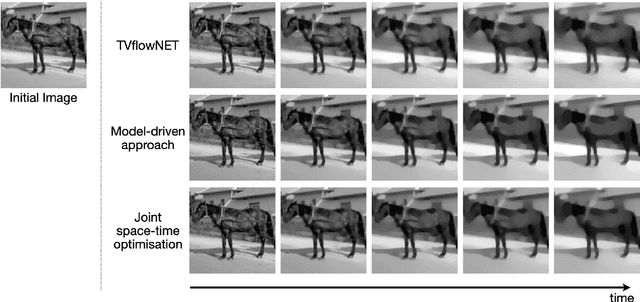
The total variation (TV) flow generates a scale-space representation of an image based on the TV functional. This gradient flow observes desirable features for images such as sharp edges and enables spectral, scale, and texture analysis. The standard numerical approach for TV flow requires solving multiple non-smooth optimisation problems. Even with state-of-the-art convex optimisation techniques, this is often prohibitively expensive and strongly motivates the use of alternative, faster approaches. Inspired by and extending the framework of physics-informed neural networks (PINNs), we propose the TVflowNET, a neural network approach to compute the solution of the TV flow given an initial image and a time instance. We significantly speed up the computation time by more than one order of magnitude and show that the TVflowNET approximates the TV flow solution with high fidelity. This is a preliminary report, more details are to follow.

Deeply Learned Spectral Total Variation Decomposition

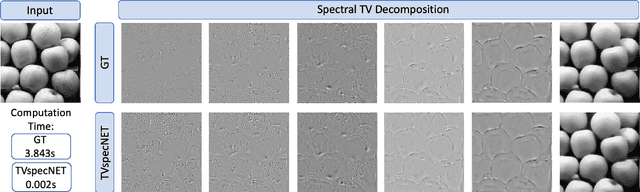
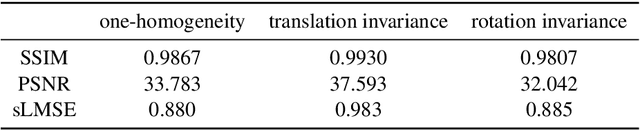
Non-linear spectral decompositions of images based on one-homogeneous functionals such as total variation have gained considerable attention in the last few years. Due to their ability to extract spectral components corresponding to objects of different size and contrast, such decompositions enable filtering, feature transfer, image fusion and other applications. However, obtaining this decomposition involves solving multiple non-smooth optimisation problems and is therefore computationally highly intensive. In this paper, we present a neural network approximation of a non-linear spectral decomposition. We report up to four orders of magnitude ($\times 10,000$) speedup in processing of mega-pixel size images, compared to classical GPU implementations. Our proposed network, TVSpecNET, is able to implicitly learn the underlying PDE and, despite being entirely data driven, inherits invariances of the model based transform. To the best of our knowledge, this is the first approach towards learning a non-linear spectral decomposition of images. Not only do we gain a staggering computational advantage, but this approach can also be seen as a step towards studying neural networks that can decompose an image into spectral components defined by a user rather than a handcrafted functional.