Weakly Convex Regularisers for Inverse Problems: Convergence of Critical Points and Primal-Dual Optimisation

Variational regularisation is the primary method for solving inverse problems, and recently there has been considerable work leveraging deeply learned regularisation for enhanced performance. However, few results exist addressing the convergence of such regularisation, particularly within the context of critical points as opposed to global minima. In this paper, we present a generalised formulation of convergent regularisation in terms of critical points, and show that this is achieved by a class of weakly convex regularisers. We prove convergence of the primal-dual hybrid gradient method for the associated variational problem, and, given a Kurdyka-Lojasiewicz condition, an $\mathcal{O}(\log{k}/k)$ ergodic convergence rate. Finally, applying this theory to learned regularisation, we prove universal approximation for input weakly convex neural networks (IWCNN), and show empirically that IWCNNs can lead to improved performance of learned adversarial regularisers for computed tomography (CT) reconstruction.

Provably Convergent Data-Driven Convex-Nonconvex Regularization

An emerging new paradigm for solving inverse problems is via the use of deep learning to learn a regularizer from data. This leads to high-quality results, but often at the cost of provable guarantees. In this work, we show how well-posedness and convergent regularization arises within the convex-nonconvex (CNC) framework for inverse problems. We introduce a novel input weakly convex neural network (IWCNN) construction to adapt the method of learned adversarial regularization to the CNC framework. Empirically we show that our method overcomes numerical issues of previous adversarial methods.

Joint reconstruction-segmentation on graphs

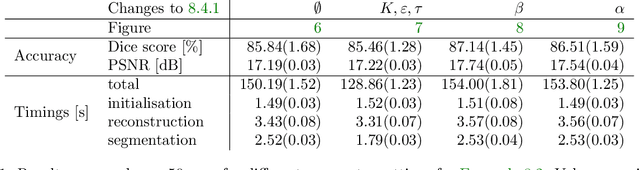
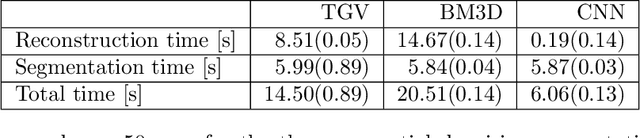
Practical image segmentation tasks concern images which must be reconstructed from noisy, distorted, and/or incomplete observations. A recent approach for solving such tasks is to perform this reconstruction jointly with the segmentation, using each to guide the other. However, this work has so far employed relatively simple segmentation methods, such as the Chan--Vese algorithm. In this paper, we present a method for joint reconstruction-segmentation using graph-based segmentation methods, which have been seeing increasing recent interest. Complications arise due to the large size of the matrices involved, and we show how these complications can be managed. We then analyse the convergence properties of our scheme. Finally, we apply this scheme to distorted versions of ``two cows'' images familiar from previous graph-based segmentation literature, first to a highly noised version and second to a blurred version, achieving highly accurate segmentations in both cases. We compare these results to those obtained by sequential reconstruction-segmentation approaches, finding that our method competes with, or even outperforms, those approaches in terms of reconstruction and segmentation accuracy.