An optimal Petrov-Galerkin framework for operator networks

The optimal Petrov-Galerkin formulation to solve partial differential equations (PDEs) recovers the best approximation in a specified finite-dimensional (trial) space with respect to a suitable norm. However, the recovery of this optimal solution is contingent on being able to construct the optimal weighting functions associated with the trial basis. While explicit constructions are available for simple one- and two-dimensional problems, such constructions for a general multidimensional problem remain elusive. In the present work, we revisit the optimal Petrov-Galerkin formulation through the lens of deep learning. We propose an operator network framework called Petrov-Galerkin Variationally Mimetic Operator Network (PG-VarMiON), which emulates the optimal Petrov-Galerkin weak form of the underlying PDE. The PG-VarMiON is trained in a supervised manner using a labeled dataset comprising the PDE data and the corresponding PDE solution, with the training loss depending on the choice of the optimal norm. The special architecture of the PG-VarMiON allows it to implicitly learn the optimal weighting functions, thus endowing the proposed operator network with the ability to generalize well beyond the training set. We derive approximation error estimates for PG-VarMiON, highlighting the contributions of various error sources, particularly the error in learning the true weighting functions. Several numerical results are presented for the advection-diffusion equation to demonstrate the efficacy of the proposed method. By embedding the Petrov-Galerkin structure into the network architecture, PG-VarMiON exhibits greater robustness and improved generalization compared to other popular deep operator frameworks, particularly when the training data is limited.

Neural Green's Operators for Parametric Partial Differential Equations

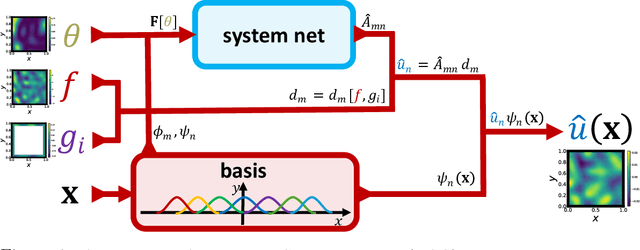
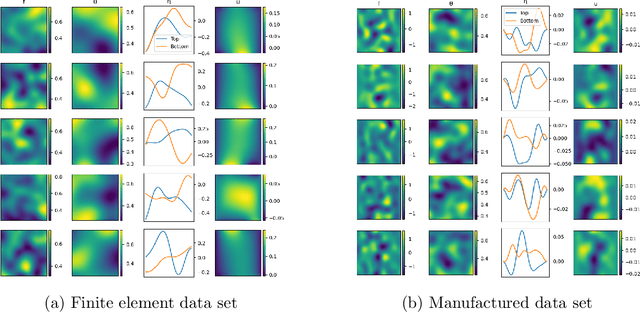
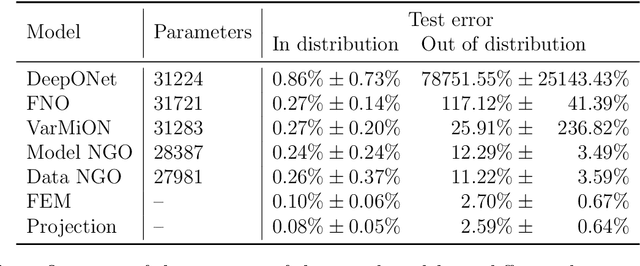
This work introduces neural Green's operators (NGOs), a novel neural operator network architecture that learns the solution operator for a parametric family of linear partial differential equations (PDEs). Our construction of NGOs is derived directly from the Green's formulation of such a solution operator. Similar to deep operator networks (DeepONets) and variationally mimetic operator networks (VarMiONs), NGOs constitutes an expansion of the solution to the PDE in terms of basis functions, that is returned from a sub-network, contracted with coefficients, that are returned from another sub-network. However, in accordance with the Green's formulation, NGOs accept weighted averages of the input functions, rather than sampled values thereof, as is the case in DeepONets and VarMiONs. Application of NGOs to canonical linear parametric PDEs shows that, while they remain competitive with DeepONets, VarMiONs and Fourier neural operators when testing on data that lie within the training distribution, they robustly generalize when testing on finer-scale data generated outside of the training distribution. Furthermore, we show that the explicit representation of the Green's function that is returned by NGOs enables the construction of effective preconditioners for numerical solvers for PDEs.

Comparison of neural closure models for discretised PDEs

Neural closure models have recently been proposed as a method for efficiently approximating small scales in multiscale systems with neural networks. The choice of loss function and associated training procedure has a large effect on the accuracy and stability of the resulting neural closure model. In this work, we systematically compare three distinct procedures: "derivative fitting", "trajectory fitting" with discretise-then-optimise, and "trajectory fitting" with optimise-then-discretise. Derivative fitting is conceptually the simplest and computationally the most efficient approach and is found to perform reasonably well on one of the test problems (Kuramoto-Sivashinsky) but poorly on the other (Burgers). Trajectory fitting is computationally more expensive but is more robust and is therefore the preferred approach. Of the two trajectory fitting procedures, the discretise-then-optimise approach produces more accurate models than the optimise-then-discretise approach. While the optimise-then-discretise approach can still produce accurate models, care must be taken in choosing the length of the trajectories used for training, in order to train the models on long-term behaviour while still producing reasonably accurate gradients during training. Two existing theorems are interpreted in a novel way that gives insight into the long-term accuracy of a neural closure model based on how accurate it is in the short term.