Thomas J. R. Hughes
An optimal Petrov-Galerkin framework for operator networks
Mar 06, 2025Abstract:The optimal Petrov-Galerkin formulation to solve partial differential equations (PDEs) recovers the best approximation in a specified finite-dimensional (trial) space with respect to a suitable norm. However, the recovery of this optimal solution is contingent on being able to construct the optimal weighting functions associated with the trial basis. While explicit constructions are available for simple one- and two-dimensional problems, such constructions for a general multidimensional problem remain elusive. In the present work, we revisit the optimal Petrov-Galerkin formulation through the lens of deep learning. We propose an operator network framework called Petrov-Galerkin Variationally Mimetic Operator Network (PG-VarMiON), which emulates the optimal Petrov-Galerkin weak form of the underlying PDE. The PG-VarMiON is trained in a supervised manner using a labeled dataset comprising the PDE data and the corresponding PDE solution, with the training loss depending on the choice of the optimal norm. The special architecture of the PG-VarMiON allows it to implicitly learn the optimal weighting functions, thus endowing the proposed operator network with the ability to generalize well beyond the training set. We derive approximation error estimates for PG-VarMiON, highlighting the contributions of various error sources, particularly the error in learning the true weighting functions. Several numerical results are presented for the advection-diffusion equation to demonstrate the efficacy of the proposed method. By embedding the Petrov-Galerkin structure into the network architecture, PG-VarMiON exhibits greater robustness and improved generalization compared to other popular deep operator frameworks, particularly when the training data is limited.
Variationally Mimetic Operator Networks
Sep 26, 2022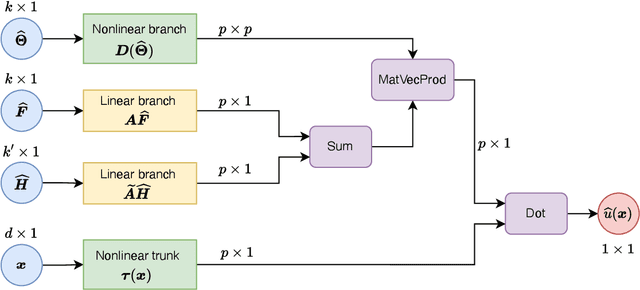

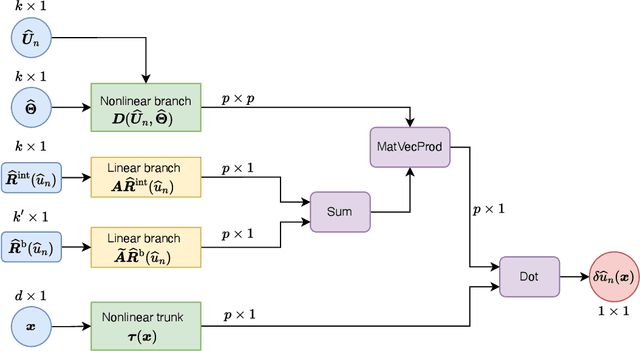
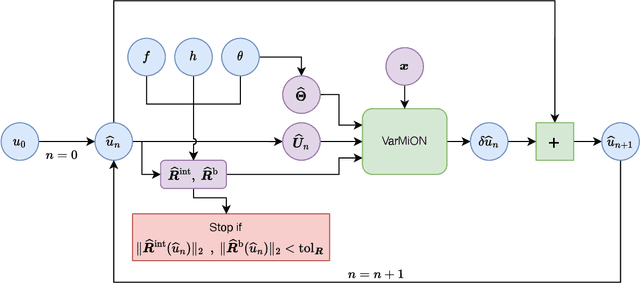
Abstract:Operator networks have emerged as promising deep learning tools for approximating the solution to partial differential equations (PDEs). These networks map input functions that describe material properties, forcing functions and boundary data to the solution of a PDE. This work describes a new architecture for operator networks that mimics the form of the numerical solution obtained from an approximation of the variational or weak formulation of the problem. The application of these ideas to a generic elliptic PDE leads to a variationally mimetic operator network (VarMiON). Like the conventional Deep Operator Network (DeepONet) the VarMiON is also composed of a sub-network that constructs the basis functions for the output and another that constructs the coefficients for these basis functions. However, in contrast to the DeepONet, in the VarMiON the architecture of these networks is precisely determined. An analysis of the error in the VarMiON solution reveals that it contains contributions from the error in the training data, the training error, quadrature error in sampling input and output functions, and a "covering error" that measures the distance between the test input functions and the nearest functions in the training dataset. It also depends on the stability constants for the exact network and its VarMiON approximation. The application of the VarMiON to a canonical elliptic PDE reveals that for approximately the same number of network parameters, on average the VarMiON incurs smaller errors than a standard DeepONet. Further, its performance is more robust to variations in input functions, the techniques used to sample the input and output functions, the techniques used to construct the basis functions, and the number of input functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge