Equivariant Flow Matching for Symmetry-Breaking Bifurcation Problems

Bifurcation phenomena in nonlinear dynamical systems often lead to multiple coexisting stable solutions, particularly in the presence of symmetry breaking. Deterministic machine learning models struggle to capture this multiplicity, averaging over solutions and failing to represent lower-symmetry outcomes. In this work, we propose a generative framework based on flow matching to model the full probability distribution over bifurcation outcomes. Our method enables direct sampling of multiple valid solutions while preserving system symmetries through equivariant modeling. We introduce a symmetric matching strategy that aligns predicted and target outputs under group actions, allowing accurate learning in equivariant settings. We validate our approach on a range of systems, from toy models to complex physical problems such as buckling beams and the Allen-Cahn equation. Our results demonstrate that flow matching significantly outperforms non-probabilistic and variational methods in capturing multimodal distributions and symmetry-breaking bifurcations, offering a principled and scalable solution for modeling multistability in high-dimensional systems.

Score Matching on Large Geometric Graphs for Cosmology Generation

Generative models are a promising tool to produce cosmological simulations but face significant challenges in scalability, physical consistency, and adherence to domain symmetries, limiting their utility as alternatives to $N$-body simulations. To address these limitations, we introduce a score-based generative model with an equivariant graph neural network that simulates gravitational clustering of galaxies across cosmologies starting from an informed prior, respects periodic boundaries, and scales to full galaxy counts in simulations. A novel topology-aware noise schedule, crucial for large geometric graphs, is introduced. The proposed equivariant score-based model successfully generates full-scale cosmological point clouds of up to 600,000 halos, respects periodicity and a uniform prior, and outperforms existing diffusion models in capturing clustering statistics while offering significant computational advantages. This work advances cosmology by introducing a generative model designed to closely resemble the underlying gravitational clustering of structure formation, moving closer to physically realistic and efficient simulators for the evolution of large-scale structures in the universe.

Flow Matching for Geometric Trajectory Simulation

The simulation of N-body systems is a fundamental problem with applications in a wide range of fields, such as molecular dynamics, biochemistry, and pedestrian dynamics. Machine learning has become an invaluable tool for scaling physics-based simulators and developing models directly from experimental data. In particular, recent advances based on deep generative modeling and geometric deep learning have enabled probabilistic simulation by modeling complex distributions over trajectories while respecting the permutation symmetry that is fundamental to N-body systems. However, to generate realistic trajectories, existing methods must learn complex transformations starting from uninformed noise and do not allow for the exploitation of domain-informed priors. In this work, we propose STFlow to address this limitation. By leveraging flow matching and data-dependent couplings, STFlow facilitates physics-informed simulation of geometric trajectories without sacrificing model expressivity or scalability. Our evaluation on N-body dynamical systems, molecular dynamics, and pedestrian dynamics benchmarks shows that STFlow produces significantly lower prediction errors while enabling more efficient inference, highlighting the benefits of employing physics-informed prior distributions in probabilistic geometric trajectory modeling.

Plasma State Monitoring and Disruption Characterization using Multimodal VAEs

When a plasma disrupts in a tokamak, significant heat and electromagnetic loads are deposited onto the surrounding device components. These forces scale with plasma current and magnetic field strength, making disruptions one of the key challenges for future devices. Unfortunately, disruptions are not fully understood, with many different underlying causes that are difficult to anticipate. Data-driven models have shown success in predicting them, but they only provide limited interpretability. On the other hand, large-scale statistical analyses have been a great asset to understanding disruptive patterns. In this paper, we leverage data-driven methods to find an interpretable representation of the plasma state for disruption characterization. Specifically, we use a latent variable model to represent diagnostic measurements as a low-dimensional, latent representation. We build upon the Variational Autoencoder (VAE) framework, and extend it for (1) continuous projections of plasma trajectories; (2) a multimodal structure to separate operating regimes; and (3) separation with respect to disruptive regimes. Subsequently, we can identify continuous indicators for the disruption rate and the disruptivity based on statistical properties of measurement data. The proposed method is demonstrated using a dataset of approximately 1600 TCV discharges, selecting for flat-top disruptions or regular terminations. We evaluate the method with respect to (1) the identified disruption risk and its correlation with other plasma properties; (2) the ability to distinguish different types of disruptions; and (3) downstream analyses. For the latter, we conduct a demonstrative study on identifying parameters connected to disruptions using counterfactual-like analysis. Overall, the method can adequately identify distinct operating regimes characterized by varying proximity to disruptions in an interpretable manner.

Robust Confinement State Classification with Uncertainty Quantification through Ensembled Data-Driven Methods

Maximizing fusion performance in tokamaks relies on high energy confinement, often achieved through distinct operating regimes. The automated labeling of these confinement states is crucial to enable large-scale analyses or for real-time control applications. While this task becomes difficult to automate near state transitions or in marginal scenarios, much success has been achieved with data-driven models. However, these methods generally provide predictions as point estimates, and cannot adequately deal with missing and/or broken input signals. To enable wide-range applicability, we develop methods for confinement state classification with uncertainty quantification and model robustness. We focus on off-line analysis for TCV discharges, distinguishing L-mode, H-mode, and an in-between dithering phase (D). We propose ensembling data-driven methods on two axes: model formulations and feature sets. The former considers a dynamic formulation based on a recurrent Fourier Neural Operator-architecture and a static formulation based on gradient-boosted decision trees. These models are trained using multiple feature groupings categorized by diagnostic system or physical quantity. A dataset of 302 TCV discharges is fully labeled, and will be publicly released. We evaluate our method quantitatively using Cohen's kappa coefficient for predictive performance and the Expected Calibration Error for the uncertainty calibration. Furthermore, we discuss performance using a variety of common and alternative scenarios, the performance of individual components, out-of-distribution performance, cases of broken or missing signals, and evaluate conditionally-averaged behavior around different state transitions. Overall, the proposed method can distinguish L, D and H-mode with high performance, can cope with missing or broken signals, and provides meaningful uncertainty estimates.

Deep Neural Cellular Potts Models

The cellular Potts model (CPM) is a powerful computational method for simulating collective spatiotemporal dynamics of biological cells. To drive the dynamics, CPMs rely on physics-inspired Hamiltonians. However, as first principles remain elusive in biology, these Hamiltonians only approximate the full complexity of real multicellular systems. To address this limitation, we propose NeuralCPM, a more expressive cellular Potts model that can be trained directly on observational data. At the core of NeuralCPM lies the Neural Hamiltonian, a neural network architecture that respects universal symmetries in collective cellular dynamics. Moreover, this approach enables seamless integration of domain knowledge by combining known biological mechanisms and the expressive Neural Hamiltonian into a hybrid model. Our evaluation with synthetic and real-world multicellular systems demonstrates that NeuralCPM is able to model cellular dynamics that cannot be accounted for by traditional analytical Hamiltonians.

Aspect-Based Few-Shot Learning

We generalize the formulation of few-shot learning by introducing the concept of an aspect. In the traditional formulation of few-shot learning, there is an underlying assumption that a single "true" label defines the content of each data point. This label serves as a basis for the comparison between the query object and the objects in the support set. However, when a human expert is asked to execute the same task without a predefined set of labels, they typically consider the rest of the data points in the support set as context. This context specifies the level of abstraction and the aspect from which the comparison can be made. In this work, we introduce a novel architecture and training procedure that develops a context given the query and support set and implements aspect-based few-shot learning that is not limited to a predetermined set of classes. We demonstrate that our method is capable of forming and using an aspect for few-shot learning on the Geometric Shapes and Sprites dataset. The results validate the feasibility of our approach compared to traditional few-shot learning.

Understanding complex crowd dynamics with generative neural simulators

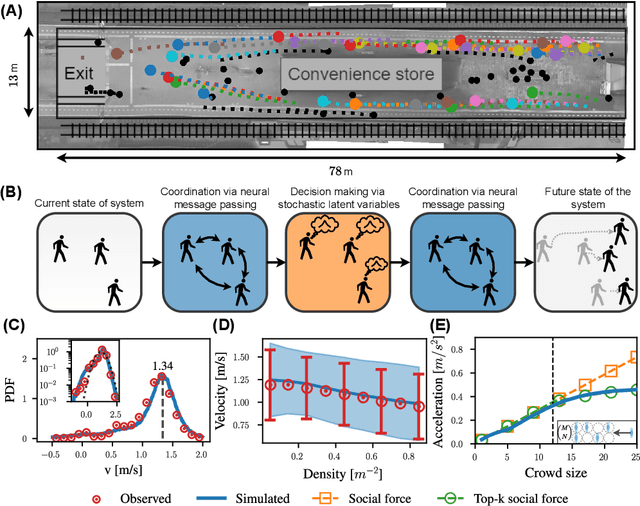
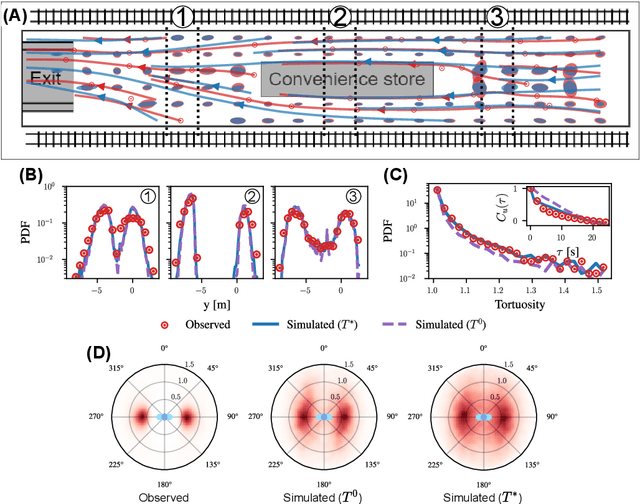
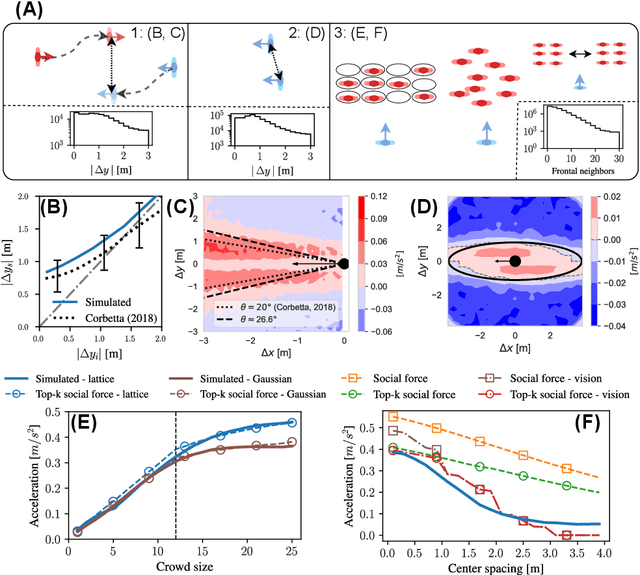
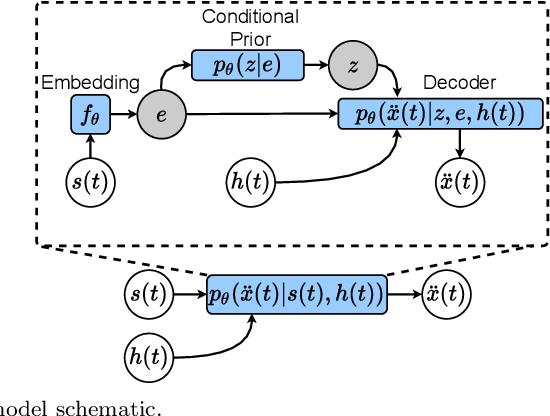
Understanding the dynamics of pedestrian crowds is an outstanding challenge crucial for designing efficient urban infrastructure and ensuring safe crowd management. To this end, both small-scale laboratory and large-scale real-world measurements have been used. However, these approaches respectively lack statistical resolution and parametric controllability, both essential to discovering physical relationships underlying the complex stochastic dynamics of crowds. Here, we establish an investigation paradigm that offers laboratory-like controllability, while ensuring the statistical resolution of large-scale real-world datasets. Using our data-driven Neural Crowd Simulator (NeCS), which we train on large-scale data and validate against key statistical features of crowd dynamics, we show that we can perform effective surrogate crowd dynamics experiments without training on specific scenarios. We not only reproduce known experimental results on pairwise avoidance, but also uncover the vision-guided and topological nature of N-body interactions. These findings show how virtual experiments based on neural simulation enable data-driven scientific discovery.

Topological degree as a discrete diagnostic for disentanglement, with applications to the $Δ$VAE

We investigate the ability of Diffusion Variational Autoencoder ($\Delta$VAE) with unit sphere $\mathcal{S}^2$ as latent space to capture topological and geometrical structure and disentangle latent factors in datasets. For this, we introduce a new diagnostic of disentanglement: namely the topological degree of the encoder, which is a map from the data manifold to the latent space. By using tools from homology theory, we derive and implement an algorithm that computes this degree. We use the algorithm to compute the degree of the encoder of models that result from the training procedure. Our experimental results show that the $\Delta$VAE achieves relatively small LSBD scores, and that regardless of the degree after initialization, the degree of the encoder after training becomes $-1$ or $+1$, which implies that the resulting encoder is at least homotopic to a homeomorphism.

Accelerating Simulation of Two-Phase Flows with Neural PDE Surrogates

Simulation is a powerful tool to better understand physical systems, but generally requires computationally expensive numerical methods. Downstream applications of such simulations can become computationally infeasible if they require many forward solves, for example in the case of inverse design with many degrees of freedom. In this work, we investigate and extend neural PDE solvers as a tool to aid in scaling simulations for two-phase flow problems, and simulations of oil expulsion from a pore specifically. We extend existing numerical methods for this problem to a more complex setting involving varying geometries of the domain to generate a challenging dataset. Further, we investigate three prominent neural PDE solver methods, namely the UNet, DRN and U-FNO, and extend them for characteristics of the oil-expulsion problem: (1) spatial conditioning on the geometry; (2) periodicity in the boundary; (3) approximate mass conservation. We scale all methods and benchmark their speed-accuracy trade-off, evaluate qualitative properties, and perform an ablation study. We find that the investigated methods can accurately model the droplet dynamics with up to three orders of magnitude speed-up, that our extensions improve performance over the baselines, and that the introduced varying geometries constitute a significantly more challenging setting over the previously considered oil expulsion problem.