Homogenization with Guaranteed Bounds via Primal-Dual Physically Informed Neural Networks

Physics-informed neural networks (PINNs) have shown promise in solving partial differential equations (PDEs) relevant to multiscale modeling, but they often fail when applied to materials with discontinuous coefficients, such as media with piecewise constant properties. This paper introduces a dual formulation for the PINN framework to improve the reliability of the homogenization of periodic thermo-conductive composites, for both strong and variational (weak) formulations. The dual approach facilitates the derivation of guaranteed upper and lower error bounds, enabling more robust detection of PINN failure. We compare standard PINNs applied to smoothed material approximations with variational PINNs (VPINNs) using both spectral and neural network-based test functions. Our results indicate that while strong-form PINNs may outperform VPINNs in controlled settings, they are sensitive to material discontinuities and may fail without clear diagnostics. In contrast, VPINNs accommodate piecewise constant material parameters directly but require careful selection of test functions to avoid instability. Dual formulation serves as a reliable indicator of convergence quality, and its integration into PINN frameworks enhances their applicability to homogenization problems in micromechanics.

Equivariant Flow Matching for Symmetry-Breaking Bifurcation Problems

Bifurcation phenomena in nonlinear dynamical systems often lead to multiple coexisting stable solutions, particularly in the presence of symmetry breaking. Deterministic machine learning models struggle to capture this multiplicity, averaging over solutions and failing to represent lower-symmetry outcomes. In this work, we propose a generative framework based on flow matching to model the full probability distribution over bifurcation outcomes. Our method enables direct sampling of multiple valid solutions while preserving system symmetries through equivariant modeling. We introduce a symmetric matching strategy that aligns predicted and target outputs under group actions, allowing accurate learning in equivariant settings. We validate our approach on a range of systems, from toy models to complex physical problems such as buckling beams and the Allen-Cahn equation. Our results demonstrate that flow matching significantly outperforms non-probabilistic and variational methods in capturing multimodal distributions and symmetry-breaking bifurcations, offering a principled and scalable solution for modeling multistability in high-dimensional systems.

Similarity Equivariant Graph Neural Networks for Homogenization of Metamaterials

Soft, porous mechanical metamaterials exhibit pattern transformations that may have important applications in soft robotics, sound reduction and biomedicine. To design these innovative materials, it is important to be able to simulate them accurately and quickly, in order to tune their mechanical properties. Since conventional simulations using the finite element method entail a high computational cost, in this article we aim to develop a machine learning-based approach that scales favorably to serve as a surrogate model. To ensure that the model is also able to handle various microstructures, including those not encountered during training, we include the microstructure as part of the network input. Therefore, we introduce a graph neural network that predicts global quantities (energy, stress stiffness) as well as the pattern transformations that occur (the kinematics). To make our model as accurate and data-efficient as possible, various symmetries are incorporated into the model. The starting point is an E(n)-equivariant graph neural network (which respects translation, rotation and reflection) that has periodic boundary conditions (i.e., it is in-/equivariant with respect to the choice of RVE), is scale in-/equivariant, can simulate large deformations, and can predict scalars, vectors as well as second and fourth order tensors (specifically energy, stress and stiffness). The incorporation of scale equivariance makes the model equivariant with respect to the similarities group, of which the Euclidean group E(n) is a subgroup. We show that this network is more accurate and data-efficient than graph neural networks with fewer symmetries. To create an efficient graph representation of the finite element discretization, we use only the internal geometrical hole boundaries from the finite element mesh to achieve a better speed-up and scaling with the mesh size.

Microstructure reconstruction via artificial neural networks: A combination of causal and non-causal approach

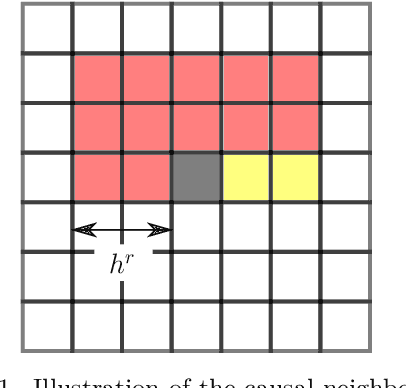
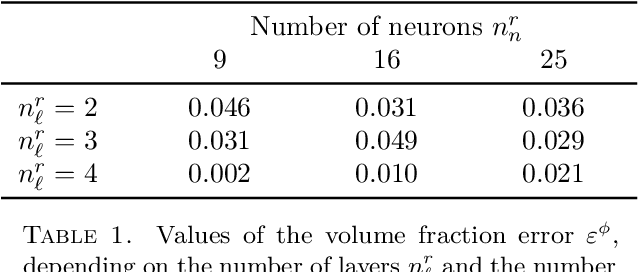
We investigate the applicability of artificial neural networks (ANNs) in reconstructing a sample image of a sponge-like microstructure. We propose to reconstruct the image by predicting the phase of the current pixel based on its causal neighbourhood, and subsequently, use a non-causal ANN model to smooth out the reconstructed image as a form of post-processing. We also consider the impacts of different configurations of the ANN model (e.g. number of densely connected layers, number of neurons in each layer, the size of both the causal and non-causal neighbourhood) on the models' predictive abilities quantified by the discrepancy between the spatial statistics of the reference and the reconstructed sample.