Plasma State Monitoring and Disruption Characterization using Multimodal VAEs

When a plasma disrupts in a tokamak, significant heat and electromagnetic loads are deposited onto the surrounding device components. These forces scale with plasma current and magnetic field strength, making disruptions one of the key challenges for future devices. Unfortunately, disruptions are not fully understood, with many different underlying causes that are difficult to anticipate. Data-driven models have shown success in predicting them, but they only provide limited interpretability. On the other hand, large-scale statistical analyses have been a great asset to understanding disruptive patterns. In this paper, we leverage data-driven methods to find an interpretable representation of the plasma state for disruption characterization. Specifically, we use a latent variable model to represent diagnostic measurements as a low-dimensional, latent representation. We build upon the Variational Autoencoder (VAE) framework, and extend it for (1) continuous projections of plasma trajectories; (2) a multimodal structure to separate operating regimes; and (3) separation with respect to disruptive regimes. Subsequently, we can identify continuous indicators for the disruption rate and the disruptivity based on statistical properties of measurement data. The proposed method is demonstrated using a dataset of approximately 1600 TCV discharges, selecting for flat-top disruptions or regular terminations. We evaluate the method with respect to (1) the identified disruption risk and its correlation with other plasma properties; (2) the ability to distinguish different types of disruptions; and (3) downstream analyses. For the latter, we conduct a demonstrative study on identifying parameters connected to disruptions using counterfactual-like analysis. Overall, the method can adequately identify distinct operating regimes characterized by varying proximity to disruptions in an interpretable manner.

A projected nonlinear state-space model for forecasting time series signals

Learning and forecasting stochastic time series is essential in various scientific fields. However, despite the proposals of nonlinear filters and deep-learning methods, it remains challenging to capture nonlinear dynamics from a few noisy samples and predict future trajectories with uncertainty estimates while maintaining computational efficiency. Here, we propose a fast algorithm to learn and forecast nonlinear dynamics from noisy time series data. A key feature of the proposed model is kernel functions applied to projected lines, enabling fast and efficient capture of nonlinearities in the latent dynamics. Through empirical case studies and benchmarking, the model demonstrates its effectiveness in learning and forecasting complex nonlinear dynamics, offering a valuable tool for researchers and practitioners in time series analysis.

Multi-Class Gaussian Process Classification Made Conjugate: Efficient Inference via Data Augmentation

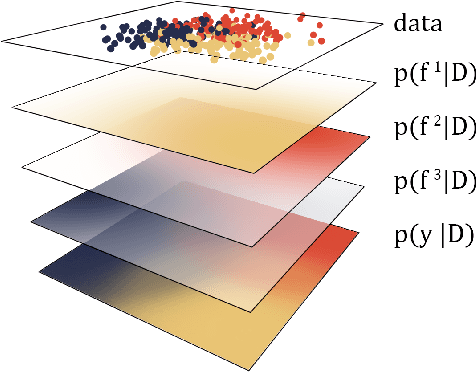
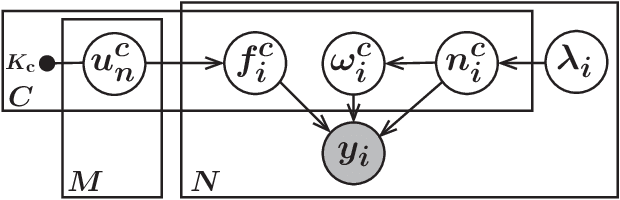
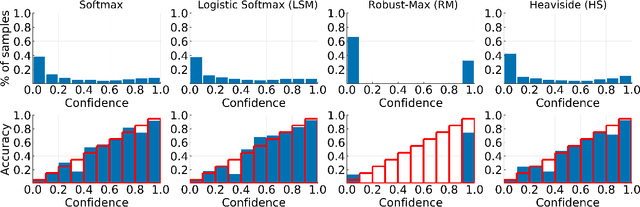
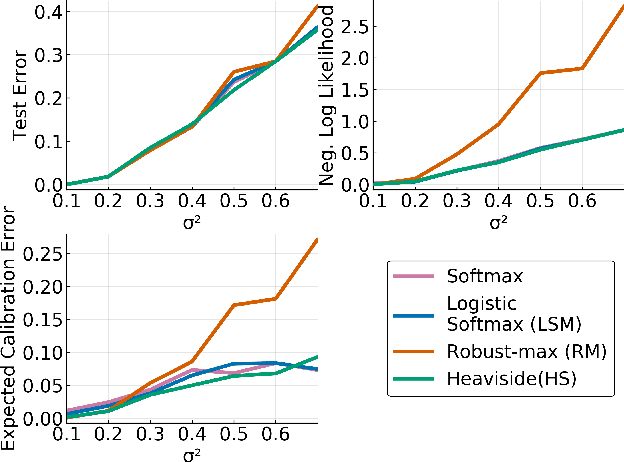
We propose a new scalable multi-class Gaussian process classification approach building on a novel modified softmax likelihood function. The new likelihood has two benefits: it leads to well-calibrated uncertainty estimates and allows for an efficient latent variable augmentation. The augmented model has the advantage that it is conditionally conjugate leading to a fast variational inference method via block coordinate ascent updates. Previous approaches suffered from a trade-off between uncertainty calibration and speed. Our experiments show that our method leads to well-calibrated uncertainty estimates and competitive predictive performance while being up to two orders faster than the state of the art.

Efficient Bayesian Inference of Sigmoidal Gaussian Cox Processes

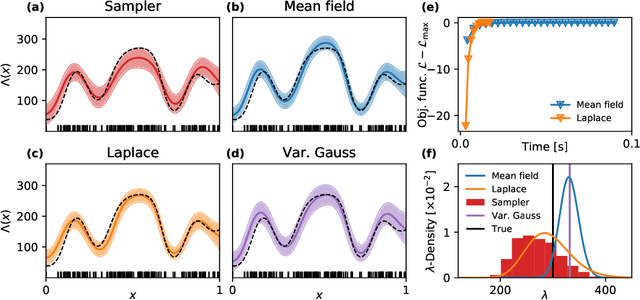
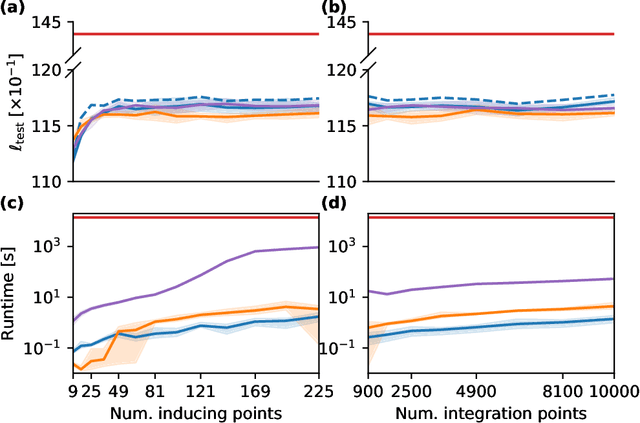
We present an approximate Bayesian inference approach for estimating the intensity of a inhomogeneous Poisson process, where the intensity function is modelled using a Gaussian process (GP) prior via a sigmoid link function. Augmenting the model using a latent marked Poisson process and P\'olya--Gamma random variables we obtain a representation of the likelihood which is conjugate to the GP prior. We approximate the posterior using a free--form mean field approximation together with the framework of sparse GPs. Furthermore, as alternative approximation we suggest a sparse Laplace approximation of the posterior, for which an efficient expectation--maximisation algorithm is derived to find the posterior's mode. Results of both algorithms compare well with exact inference obtained by a Markov Chain Monte Carlo sampler and standard variational Gauss approach, while being one order of magnitude faster.

Efficient Bayesian Inference for a Gaussian Process Density Model

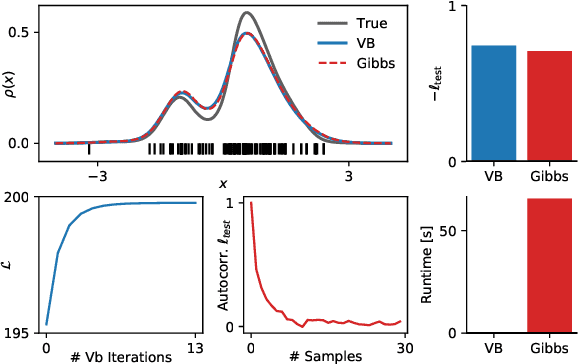
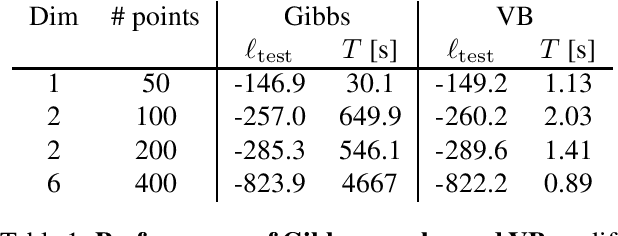
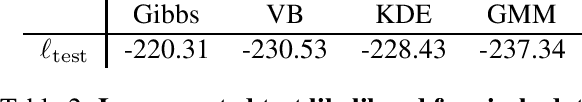
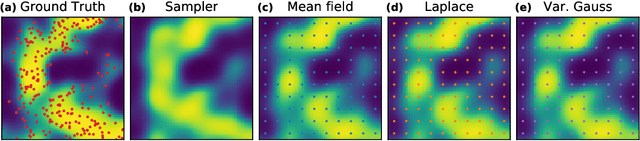
We reconsider a nonparametric density model based on Gaussian processes. By augmenting the model with latent P\'olya--Gamma random variables and a latent marked Poisson process we obtain a new likelihood which is conjugate to the model's Gaussian process prior. The augmented posterior allows for efficient inference by Gibbs sampling and an approximate variational mean field approach. For the latter we utilise sparse GP approximations to tackle the infinite dimensionality of the problem. The performance of both algorithms and comparisons with other density estimators are demonstrated on artificial and real datasets with up to several thousand data points.

Inverse Ising problem in continuous time: A latent variable approach

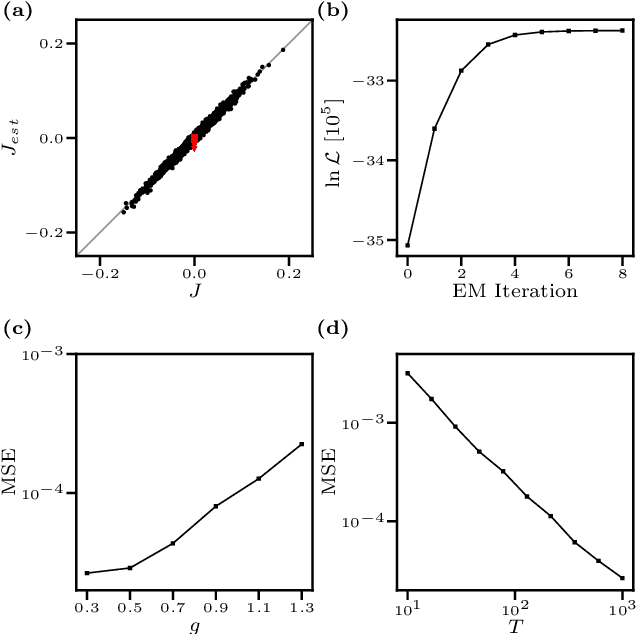
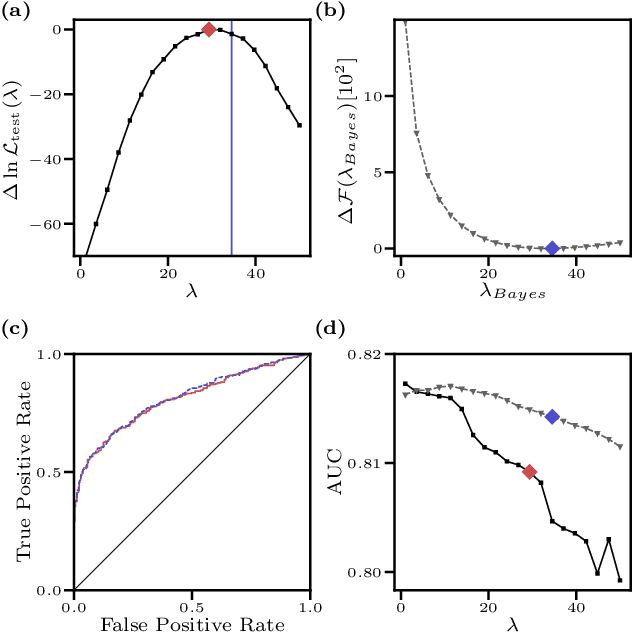
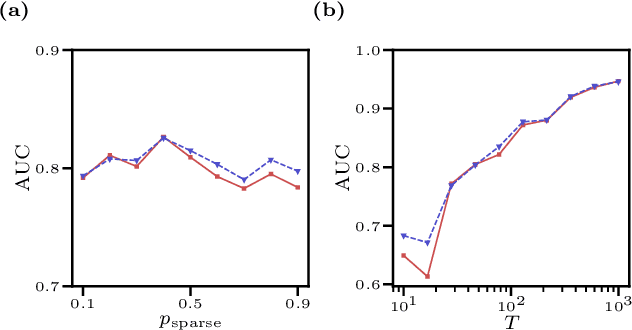
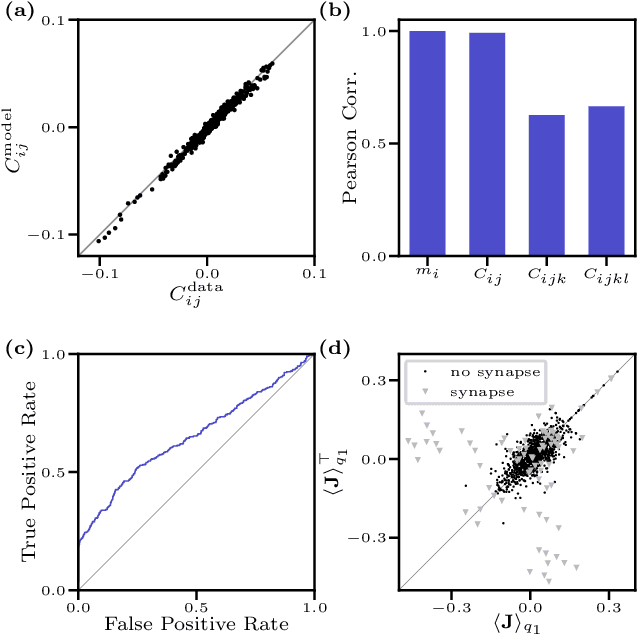
We consider the inverse Ising problem, i.e. the inference of network couplings from observed spin trajectories for a model with continuous time Glauber dynamics. By introducing two sets of auxiliary latent random variables we render the likelihood into a form, which allows for simple iterative inference algorithms with analytical updates. The variables are: (1) Poisson variables to linearise an exponential term which is typical for point process likelihoods and (2) P\'olya-Gamma variables, which make the likelihood quadratic in the coupling parameters. Using the augmented likelihood, we derive an expectation-maximization (EM) algorithm to obtain the maximum likelihood estimate of network parameters. Using a third set of latent variables we extend the EM algorithm to sparse couplings via L1 regularization. Finally, we develop an efficient approximate Bayesian inference algorithm using a variational approach. We demonstrate the performance of our algorithms on data simulated from an Ising model. For data which are simulated from a more biologically plausible network with spiking neurons, we show that the Ising model captures well the low order statistics of the data and how the Ising couplings are related to the underlying synaptic structure of the simulated network.