Adaptive Inducing Points Selection For Gaussian Processes

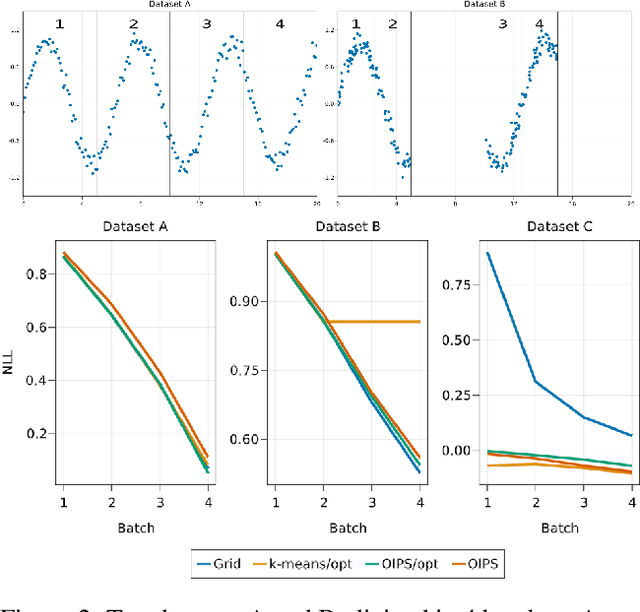
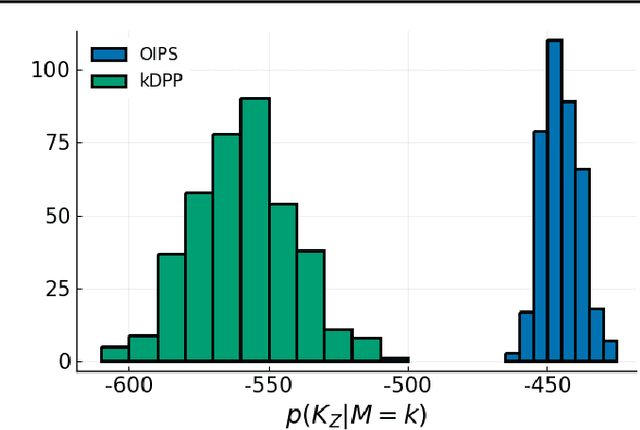
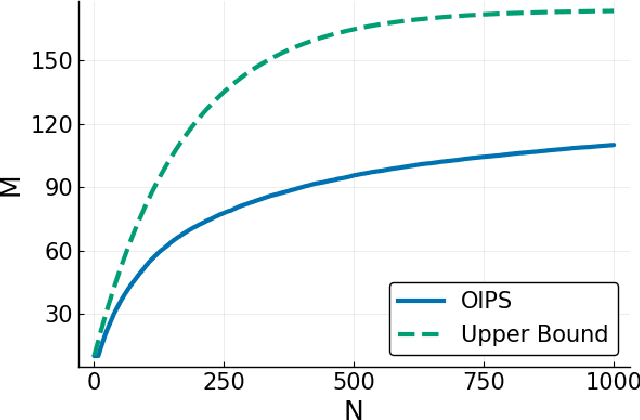
Gaussian Processes (\textbf{GPs}) are flexible non-parametric models with strong probabilistic interpretation. While being a standard choice for performing inference on time series, GPs have few techniques to work in a streaming setting. \cite{bui2017streaming} developed an efficient variational approach to train online GPs by using sparsity techniques: The whole set of observations is approximated by a smaller set of inducing points (\textbf{IPs}) and moved around with new data. Both the number and the locations of the IPs will affect greatly the performance of the algorithm. In addition to optimizing their locations, we propose to adaptively add new points, based on the properties of the GP and the structure of the data.

Automated Augmented Conjugate Inference for Non-conjugate Gaussian Process Models

We propose automated augmented conjugate inference, a new inference method for non-conjugate Gaussian processes (GP) models. Our method automatically constructs an auxiliary variable augmentation that renders the GP model conditionally conjugate. Building on the conjugate structure of the augmented model, we develop two inference methods. First, a fast and scalable stochastic variational inference method that uses efficient block coordinate ascent updates, which are computed in closed form. Second, an asymptotically correct Gibbs sampler that is useful for small datasets. Our experiments show that our method are up two orders of magnitude faster and more robust than existing state-of-the-art black-box methods.

Multi-Class Gaussian Process Classification Made Conjugate: Efficient Inference via Data Augmentation

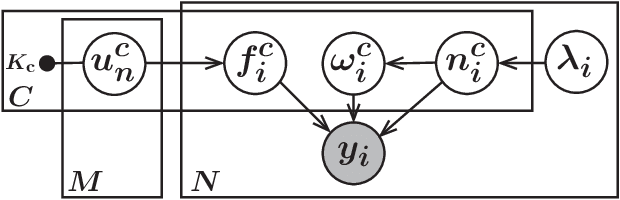
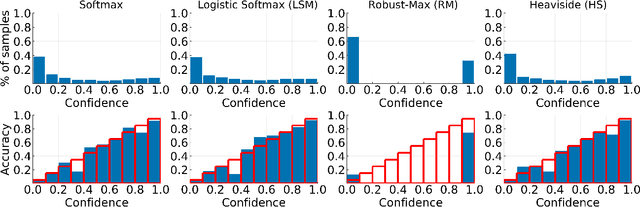
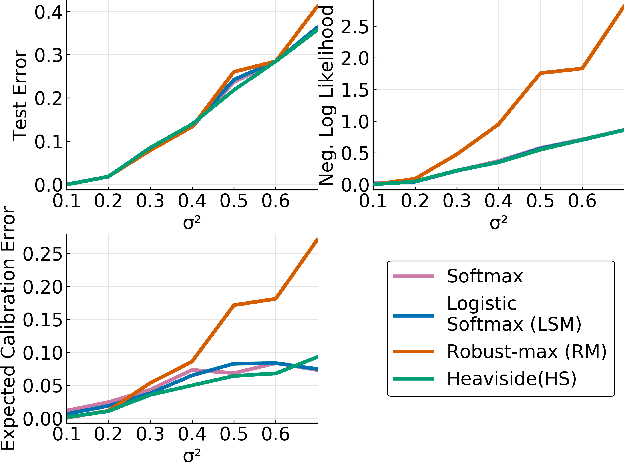
We propose a new scalable multi-class Gaussian process classification approach building on a novel modified softmax likelihood function. The new likelihood has two benefits: it leads to well-calibrated uncertainty estimates and allows for an efficient latent variable augmentation. The augmented model has the advantage that it is conditionally conjugate leading to a fast variational inference method via block coordinate ascent updates. Previous approaches suffered from a trade-off between uncertainty calibration and speed. Our experiments show that our method leads to well-calibrated uncertainty estimates and competitive predictive performance while being up to two orders faster than the state of the art.