Inverse Ising problem in continuous time: A latent variable approach
Paper and Code
Dec 21, 2017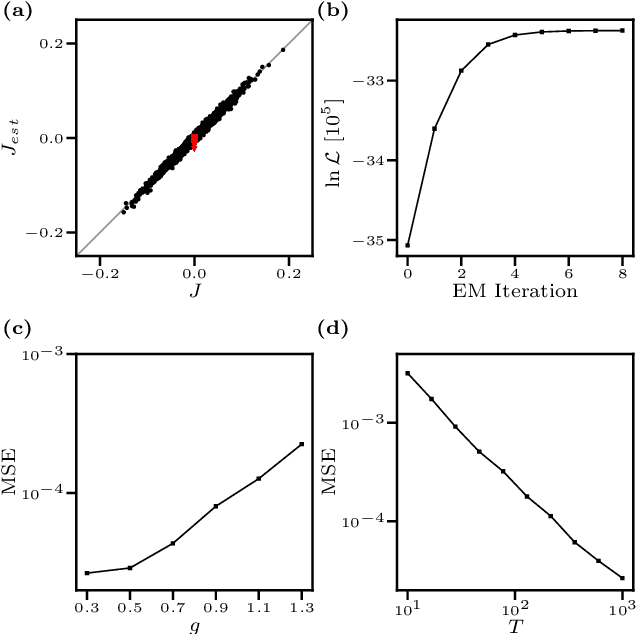
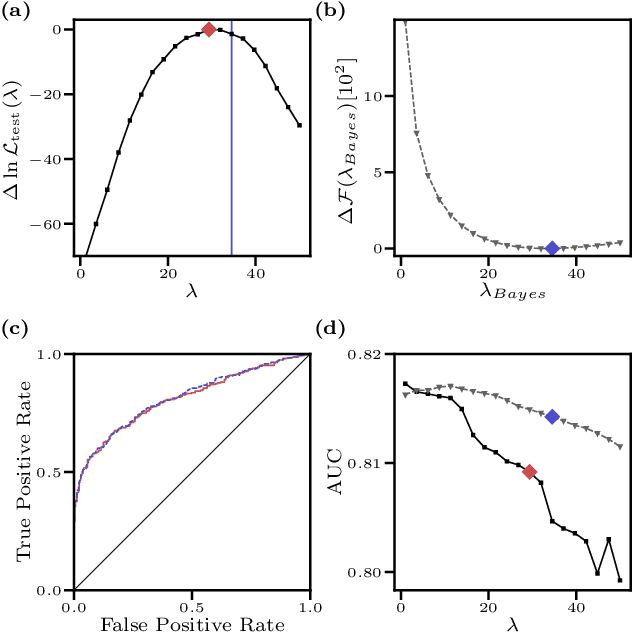
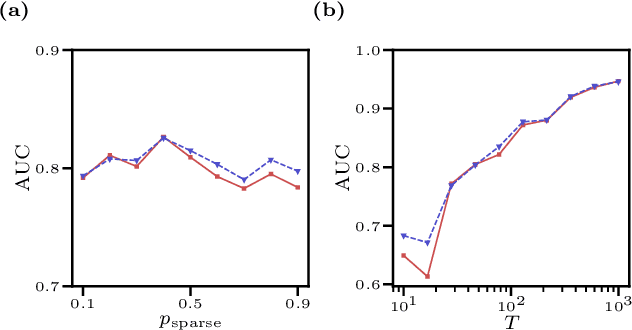
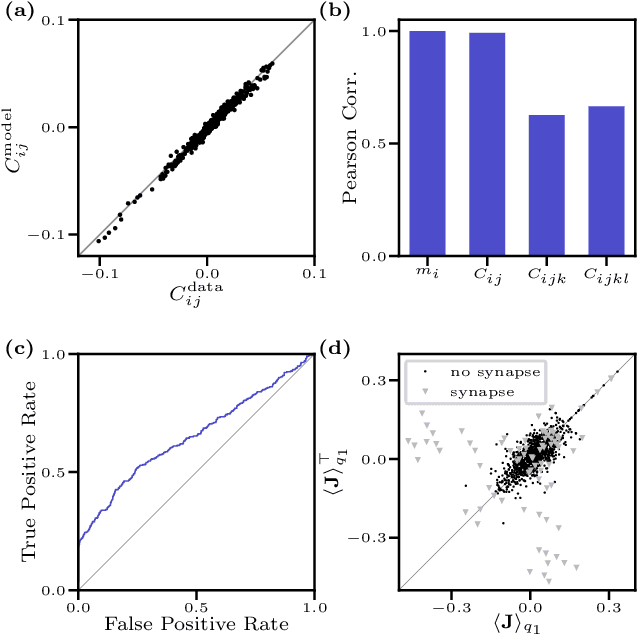
We consider the inverse Ising problem, i.e. the inference of network couplings from observed spin trajectories for a model with continuous time Glauber dynamics. By introducing two sets of auxiliary latent random variables we render the likelihood into a form, which allows for simple iterative inference algorithms with analytical updates. The variables are: (1) Poisson variables to linearise an exponential term which is typical for point process likelihoods and (2) P\'olya-Gamma variables, which make the likelihood quadratic in the coupling parameters. Using the augmented likelihood, we derive an expectation-maximization (EM) algorithm to obtain the maximum likelihood estimate of network parameters. Using a third set of latent variables we extend the EM algorithm to sparse couplings via L1 regularization. Finally, we develop an efficient approximate Bayesian inference algorithm using a variational approach. We demonstrate the performance of our algorithms on data simulated from an Ising model. For data which are simulated from a more biologically plausible network with spiking neurons, we show that the Ising model captures well the low order statistics of the data and how the Ising couplings are related to the underlying synaptic structure of the simulated network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge