Michael Abdelmalik
Neural Green's Operators for Parametric Partial Differential Equations
Jun 04, 2024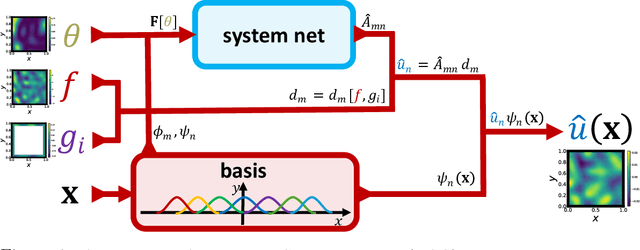

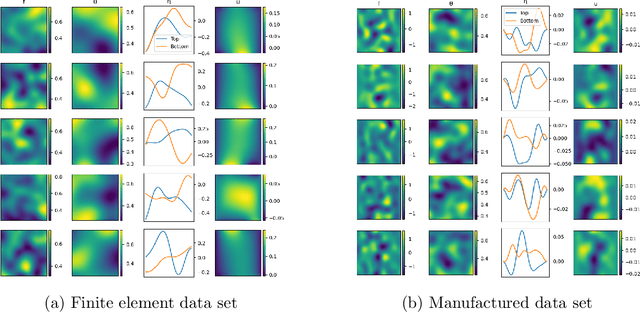
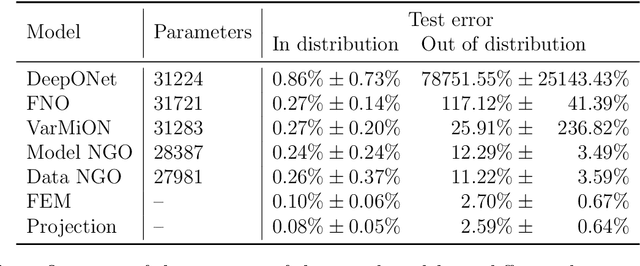
Abstract:This work introduces neural Green's operators (NGOs), a novel neural operator network architecture that learns the solution operator for a parametric family of linear partial differential equations (PDEs). Our construction of NGOs is derived directly from the Green's formulation of such a solution operator. Similar to deep operator networks (DeepONets) and variationally mimetic operator networks (VarMiONs), NGOs constitutes an expansion of the solution to the PDE in terms of basis functions, that is returned from a sub-network, contracted with coefficients, that are returned from another sub-network. However, in accordance with the Green's formulation, NGOs accept weighted averages of the input functions, rather than sampled values thereof, as is the case in DeepONets and VarMiONs. Application of NGOs to canonical linear parametric PDEs shows that, while they remain competitive with DeepONets, VarMiONs and Fourier neural operators when testing on data that lie within the training distribution, they robustly generalize when testing on finer-scale data generated outside of the training distribution. Furthermore, we show that the explicit representation of the Green's function that is returned by NGOs enables the construction of effective preconditioners for numerical solvers for PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge