Comparison of neural closure models for discretised PDEs

Neural closure models have recently been proposed as a method for efficiently approximating small scales in multiscale systems with neural networks. The choice of loss function and associated training procedure has a large effect on the accuracy and stability of the resulting neural closure model. In this work, we systematically compare three distinct procedures: "derivative fitting", "trajectory fitting" with discretise-then-optimise, and "trajectory fitting" with optimise-then-discretise. Derivative fitting is conceptually the simplest and computationally the most efficient approach and is found to perform reasonably well on one of the test problems (Kuramoto-Sivashinsky) but poorly on the other (Burgers). Trajectory fitting is computationally more expensive but is more robust and is therefore the preferred approach. Of the two trajectory fitting procedures, the discretise-then-optimise approach produces more accurate models than the optimise-then-discretise approach. While the optimise-then-discretise approach can still produce accurate models, care must be taken in choosing the length of the trajectories used for training, in order to train the models on long-term behaviour while still producing reasonably accurate gradients during training. Two existing theorems are interpreted in a novel way that gives insight into the long-term accuracy of a neural closure model based on how accurate it is in the short term.

Stochastic parameterization with VARX processes

In this study we investigate a data-driven stochastic methodology to parameterize small-scale features in a prototype multiscale dynamical system, the Lorenz '96 (L96) model. We propose to model the small-scale features using a vector autoregressive process with exogenous variable (VARX), estimated from given sample data. To reduce the number of parameters of the VARX we impose a diagonal structure on its coefficient matrices. We apply the VARX to two different configurations of the 2-layer L96 model, one with common parameter choices giving unimodal invariant probability distributions for the L96 model variables, and one with non-standard parameters giving trimodal distributions. We show through various statistical criteria that the proposed VARX performs very well for the unimodal configuration, while keeping the number of parameters linear in the number of model variables. We also show that the parameterization performs accurately for the very challenging trimodal L96 configuration by allowing for a dense (non-diagonal) VARX covariance matrix.

Resampling with neural networks for stochastic parameterization in multiscale systems

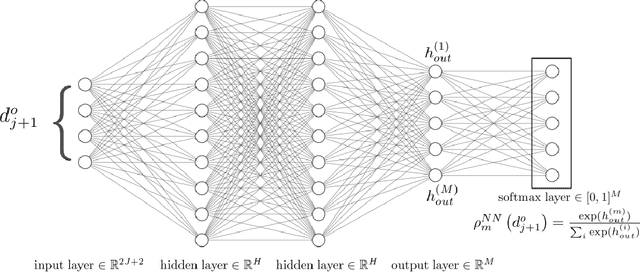
In simulations of multiscale dynamical systems, not all relevant processes can be resolved explicitly. Taking the effect of the unresolved processes into account is important, which introduces the need for paramerizations. We present a machine-learning method, used for the conditional resampling of observations or reference data from a fully resolved simulation. It is based on the probabilistic classiffcation of subsets of reference data, conditioned on macroscopic variables. This method is used to formulate a parameterization that is stochastic, taking the uncertainty of the unresolved scales into account. We validate our approach on the Lorenz 96 system, using two different parameter settings which are challenging for parameterization methods.