Energy-Conserving Neural Network Closure Model for Long-Time Accurate and Stable LES

Machine learning-based closure models for LES have shown promise in capturing complex turbulence dynamics but often suffer from instabilities and physical inconsistencies. In this work, we develop a novel skew-symmetric neural architecture as closure model that enforces stability while preserving key physical conservation laws. Our approach leverages a discretization that ensures mass, momentum, and energy conservation, along with a face-averaging filter to maintain mass conservation in coarse-grained velocity fields. We compare our model against several conventional data-driven closures (including unconstrained convolutional neural networks), and the physics-based Smagorinsky model. Performance is evaluated on decaying turbulence and Kolmogorov flow for multiple coarse-graining factors. In these test cases we observe that unconstrained machine learning models suffer from numerical instabilities. In contrast, our skew-symmetric model remains stable across all tests, though at the cost of increased dissipation. Despite this trade-off, we demonstrate that our model still outperforms the Smagorinsky model in unseen scenarios. These findings highlight the potential of structure-preserving machine learning closures for reliable long-time LES.

Sensitivity Analysis of High-Dimensional Models with Correlated Inputs

Sensitivity analysis is an important tool used in many domains of computational science to either gain insight into the mathematical model and interaction of its parameters or study the uncertainty propagation through the input-output interactions. In many applications, the inputs are stochastically dependent, which violates one of the essential assumptions in the state-of-the-art sensitivity analysis methods. Consequently, the results obtained ignoring the correlations provide values which do not reflect the true contributions of the input parameters. This study proposes an approach to address the parameter correlations using a polynomial chaos expansion method and Rosenblatt and Cholesky transformations to reflect the parameter dependencies. Treatment of the correlated variables is discussed in context of variance and derivative-based sensitivity analysis. We demonstrate that the sensitivity of the correlated parameters can not only differ in magnitude, but even the sign of the derivative-based index can be inverted, thus significantly altering the model behavior compared to the prediction of the analysis disregarding the correlations. Numerous experiments are conducted using workflow automation tools within the VECMA toolkit.

Resampling with neural networks for stochastic parameterization in multiscale systems

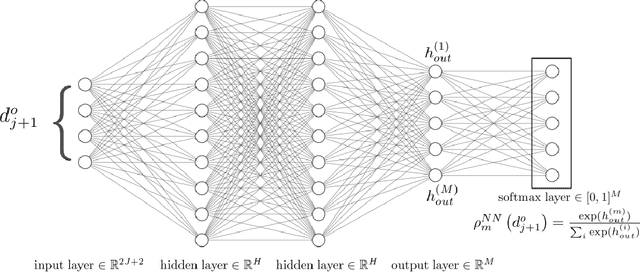
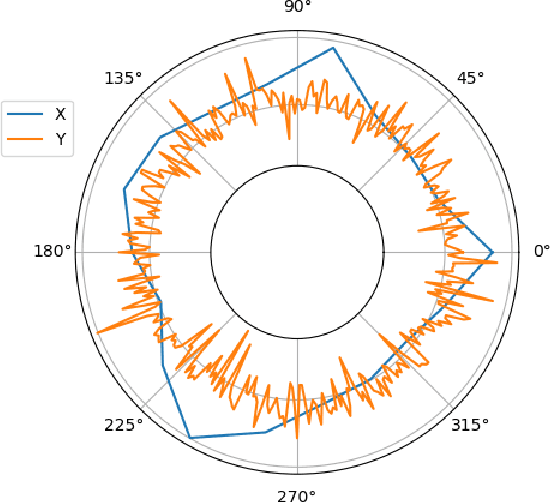
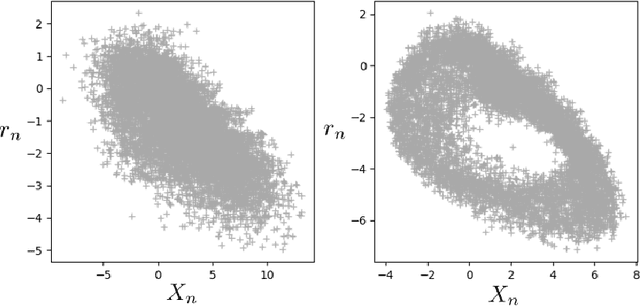
In simulations of multiscale dynamical systems, not all relevant processes can be resolved explicitly. Taking the effect of the unresolved processes into account is important, which introduces the need for paramerizations. We present a machine-learning method, used for the conditional resampling of observations or reference data from a fully resolved simulation. It is based on the probabilistic classiffcation of subsets of reference data, conditioned on macroscopic variables. This method is used to formulate a parameterization that is stochastic, taking the uncertainty of the unresolved scales into account. We validate our approach on the Lorenz 96 system, using two different parameter settings which are challenging for parameterization methods.