Building Interpretable Climate Emulators for Economics

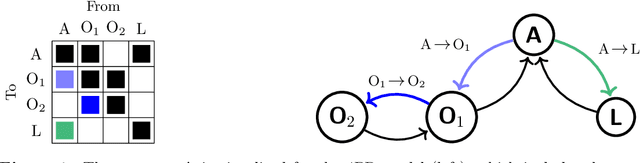
This paper presents a framework for developing efficient and interpretable carbon-cycle emulators (CCEs) as part of climate emulators in Integrated Assessment Models, enabling economists to custom-build CCEs accurately calibrated to advanced climate science. We propose a generalized multi-reservoir linear box-model CCE that preserves key physical quantities and can be use-case tailored for specific use cases. Three CCEs are presented for illustration: the 3SR model (replicating DICE-2016), the 4PR model (including the land biosphere), and the 4PR-X model (accounting for dynamic land-use changes like deforestation that impact the reservoir's storage capacity). Evaluation of these models within the DICE framework shows that land-use changes in the 4PR-X model significantly impact atmospheric carbon and temperatures -- emphasizing the importance of using tailored climate emulators. By providing a transparent and flexible tool for policy analysis, our framework allows economists to assess the economic impacts of climate policies more accurately.

Application of deep and reinforcement learning to boundary control problems

The boundary control problem is a non-convex optimization and control problem in many scientific domains, including fluid mechanics, structural engineering, and heat transfer optimization. The aim is to find the optimal values for the domain boundaries such that the enclosed domain adhering to the governing equations attains the desired state values. Traditionally, non-linear optimization methods, such as the Interior-Point method (IPM), are used to solve such problems. This project explores the possibilities of using deep learning and reinforcement learning to solve boundary control problems. We adhere to the framework of iterative optimization strategies, employing a spatial neural network to construct well-informed initial guesses, and a spatio-temporal neural network learns the iterative optimization algorithm using policy gradients. Synthetic data, generated from the problems formulated in the literature, is used for training, testing and validation. The numerical experiments indicate that the proposed method can rival the speed and accuracy of existing solvers. In our preliminary results, the network attains costs lower than IPOPT, a state-of-the-art non-linear IPM, in 51\% cases. The overall number of floating point operations in the proposed method is similar to that of IPOPT. Additionally, the informed initial guess method and the learned momentum-like behaviour in the optimizer method are incorporated to avoid convergence to local minima.

AI Driven Near Real-time Locational Marginal Pricing Method: A Feasibility and Robustness Study

Accurate price predictions are essential for market participants in order to optimize their operational schedules and bidding strategies, especially in the current context where electricity prices become more volatile and less predictable using classical approaches. Locational Marginal Pricing (LMP) pricing mechanism is used in many modern power markets, where the traditional approach utilizes optimal power flow (OPF) solvers. However, for large electricity grids this process becomes prohibitively time-consuming and computationally intensive. Machine learning solutions could provide an efficient tool for LMP prediction, especially in energy markets with intermittent sources like renewable energy. The study evaluates the performance of popular machine learning and deep learning models in predicting LMP on multiple electricity grids. The accuracy and robustness of these models in predicting LMP is assessed considering multiple scenarios. The results show that machine learning models can predict LMP 4-5 orders of magnitude faster than traditional OPF solvers with 5-6\% error rate, highlighting the potential of machine learning models in LMP prediction for large-scale power models with the help of hardware solutions like multi-core CPUs and GPUs in modern HPC clusters.

Sensitivity Analysis of High-Dimensional Models with Correlated Inputs

Sensitivity analysis is an important tool used in many domains of computational science to either gain insight into the mathematical model and interaction of its parameters or study the uncertainty propagation through the input-output interactions. In many applications, the inputs are stochastically dependent, which violates one of the essential assumptions in the state-of-the-art sensitivity analysis methods. Consequently, the results obtained ignoring the correlations provide values which do not reflect the true contributions of the input parameters. This study proposes an approach to address the parameter correlations using a polynomial chaos expansion method and Rosenblatt and Cholesky transformations to reflect the parameter dependencies. Treatment of the correlated variables is discussed in context of variance and derivative-based sensitivity analysis. We demonstrate that the sensitivity of the correlated parameters can not only differ in magnitude, but even the sign of the derivative-based index can be inverted, thus significantly altering the model behavior compared to the prediction of the analysis disregarding the correlations. Numerous experiments are conducted using workflow automation tools within the VECMA toolkit.

$K$-way $p$-spectral clustering on Grassmann manifolds

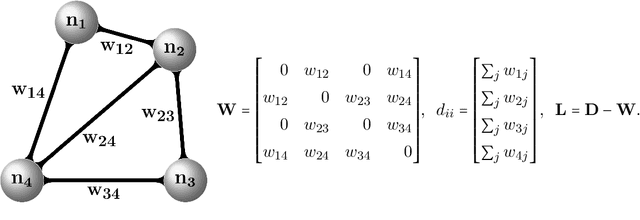
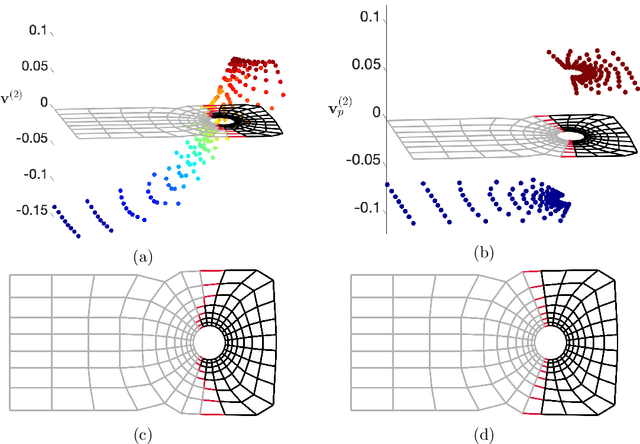
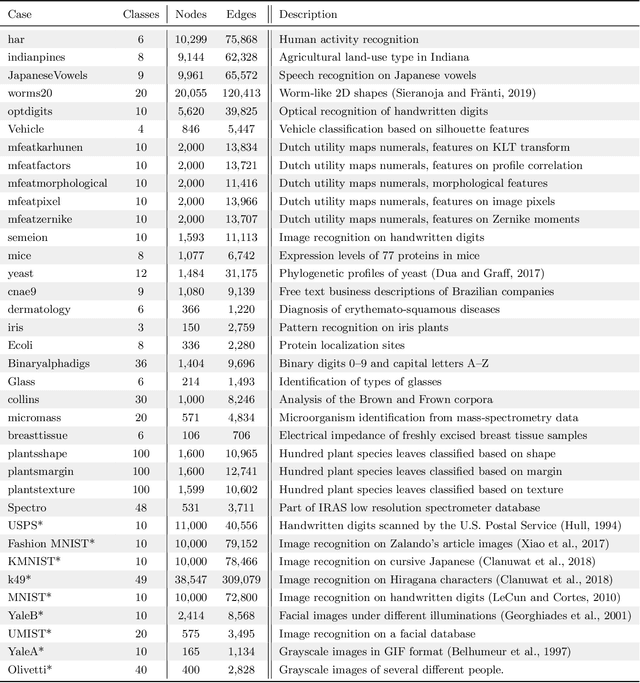
Spectral methods have gained a lot of recent attention due to the simplicity of their implementation and their solid mathematical background. We revisit spectral graph clustering, and reformulate in the $p$-norm the continuous problem of minimizing the graph Laplacian Rayleigh quotient. The value of $p \in (1,2]$ is reduced, promoting sparser solution vectors that correspond to optimal clusters as $p$ approaches one. The computation of multiple $p$-eigenvectors of the graph $p$-Laplacian, a nonlinear generalization of the standard graph Laplacian, is achieved by the minimization of our objective function on the Grassmann manifold, hence ensuring the enforcement of the orthogonality constraint between them. Our approach attempts to bridge the fields of graph clustering and nonlinear numerical optimization, and employs a robust algorithm to obtain clusters of high quality. The benefits of the suggested method are demonstrated in a plethora of artificial and real-world graphs. Our results are compared against standard spectral clustering methods and the current state-of-the-art algorithm for clustering using the graph $p$-Laplacian variant.