Harald Köstler
Agentic large language models improve retrieval-based radiology question answering
Aug 01, 2025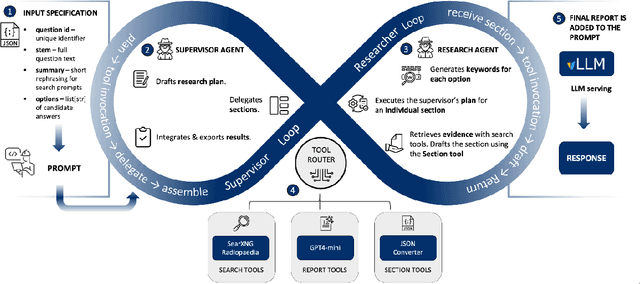
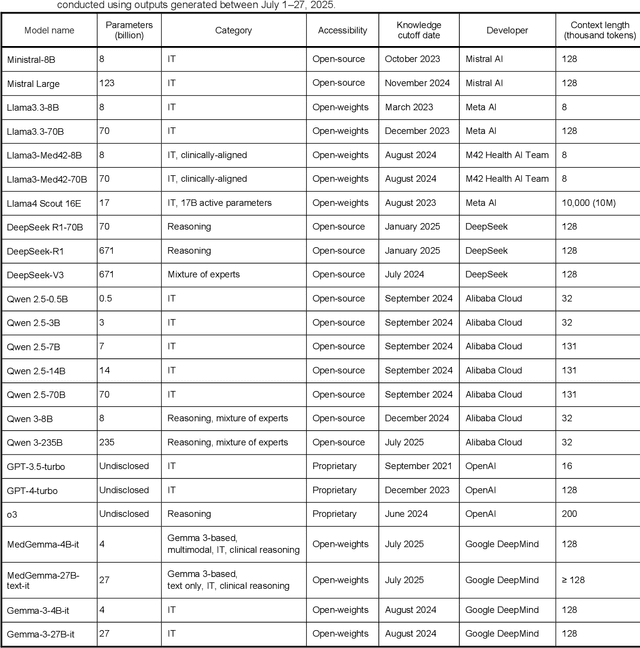
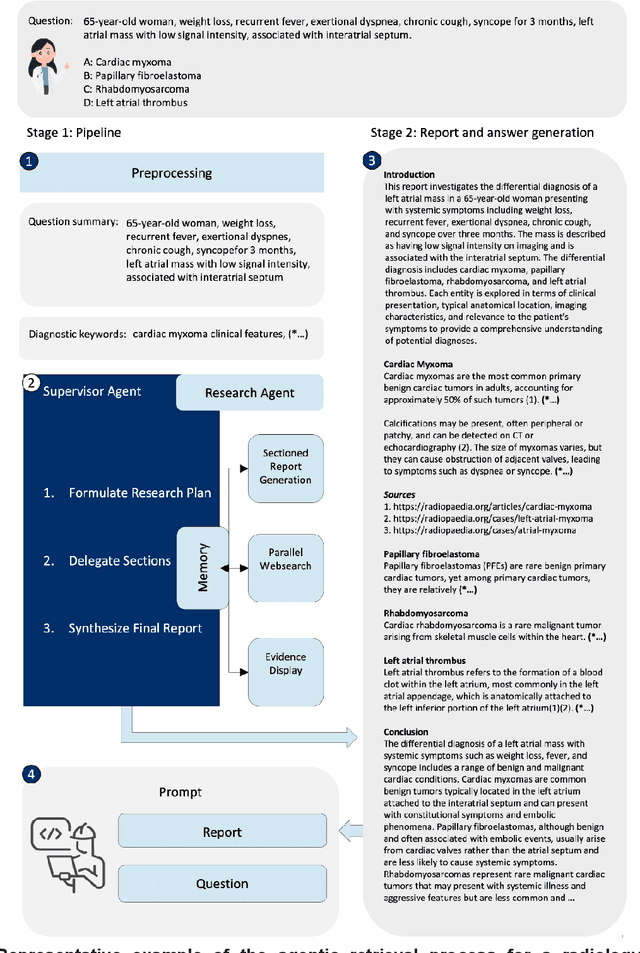
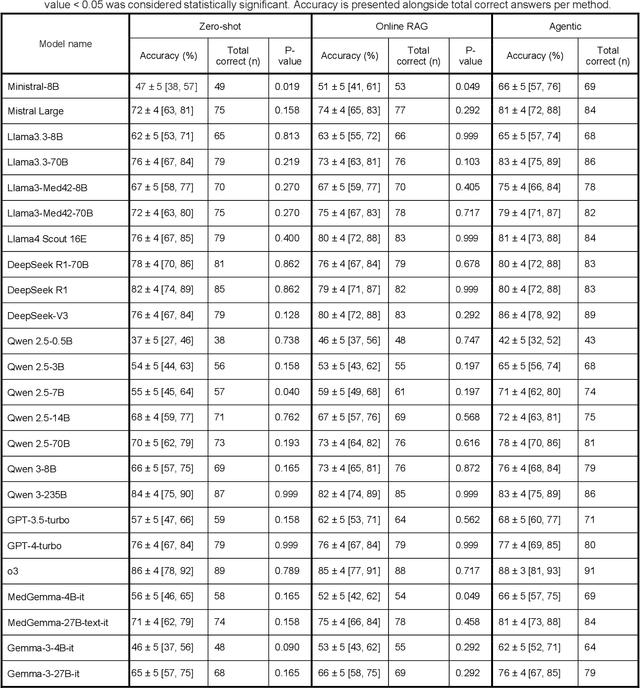
Abstract:Clinical decision-making in radiology increasingly benefits from artificial intelligence (AI), particularly through large language models (LLMs). However, traditional retrieval-augmented generation (RAG) systems for radiology question answering (QA) typically rely on single-step retrieval, limiting their ability to handle complex clinical reasoning tasks. Here we propose an agentic RAG framework enabling LLMs to autonomously decompose radiology questions, iteratively retrieve targeted clinical evidence from Radiopaedia, and dynamically synthesize evidence-based responses. We evaluated 24 LLMs spanning diverse architectures, parameter scales (0.5B to >670B), and training paradigms (general-purpose, reasoning-optimized, clinically fine-tuned), using 104 expert-curated radiology questions from previously established RSNA-RadioQA and ExtendedQA datasets. Agentic retrieval significantly improved mean diagnostic accuracy over zero-shot prompting (73% vs. 64%; P<0.001) and conventional online RAG (73% vs. 68%; P<0.001). The greatest gains occurred in mid-sized models (e.g., Mistral Large improved from 72% to 81%) and small-scale models (e.g., Qwen 2.5-7B improved from 55% to 71%), while very large models (>200B parameters) demonstrated minimal changes (<2% improvement). Additionally, agentic retrieval reduced hallucinations (mean 9.4%) and retrieved clinically relevant context in 46% of cases, substantially aiding factual grounding. Even clinically fine-tuned models exhibited meaningful improvements (e.g., MedGemma-27B improved from 71% to 81%), indicating complementary roles of retrieval and fine-tuning. These results highlight the potential of agentic frameworks to enhance factuality and diagnostic accuracy in radiology QA, particularly among mid-sized LLMs, warranting future studies to validate their clinical utility.
Benchmarking Convolutional Neural Network and Graph Neural Network based Surrogate Models on a Real-World Car External Aerodynamics Dataset
Apr 09, 2025Abstract:Aerodynamic optimization is crucial for developing eco-friendly, aerodynamic, and stylish cars, which requires close collaboration between aerodynamicists and stylists, a collaboration impaired by the time-consuming nature of aerodynamic simulations. Surrogate models offer a viable solution to reduce this overhead, but they are untested in real-world aerodynamic datasets. We present a comparative evaluation of two surrogate modeling approaches for predicting drag on a real-world dataset: a Convolutional Neural Network (CNN) model that uses a signed distance field as input and a commercial tool based on Graph Neural Networks (GNN) that directly processes a surface mesh. In contrast to previous studies based on datasets created from parameterized geometries, our dataset comprises 343 geometries derived from 32 baseline vehicle geometries across five distinct car projects, reflecting the diverse, free-form modifications encountered in the typical vehicle development process. Our results show that the CNN-based method achieves a mean absolute error of 2.3 drag counts, while the GNN-based method achieves 3.8. Both methods achieve approximately 77% accuracy in predicting the direction of drag change relative to the baseline geometry. While both methods effectively capture the broader trends between baseline groups (set of samples derived from a single baseline geometry), they struggle to varying extents in capturing the finer intra-baseline group variations. In summary, our findings suggest that aerodynamicists can effectively use both methods to predict drag in under two minutes, which is at least 600 times faster than performing a simulation. However, there remains room for improvement in capturing the finer details of the geometry.
Towards Automated Algebraic Multigrid Preconditioner Design Using Genetic Programming for Large-Scale Laser Beam Welding Simulations
Dec 11, 2024



Abstract:Multigrid methods are asymptotically optimal algorithms ideal for large-scale simulations. But, they require making numerous algorithmic choices that significantly influence their efficiency. Unlike recent approaches that learn optimal multigrid components using machine learning techniques, we adopt a complementary strategy here, employing evolutionary algorithms to construct efficient multigrid cycles from available individual components. This technology is applied to finite element simulations of the laser beam welding process. The thermo-elastic behavior is described by a coupled system of time-dependent thermo-elasticity equations, leading to nonlinear and ill-conditioned systems. The nonlinearity is addressed using Newton's method, and iterative solvers are accelerated with an algebraic multigrid (AMG) preconditioner using hypre BoomerAMG interfaced via PETSc. This is applied as a monolithic solver for the coupled equations. To further enhance solver efficiency, flexible AMG cycles are introduced, extending traditional cycle types with level-specific smoothing sequences and non-recursive cycling patterns. These are automatically generated using genetic programming, guided by a context-free grammar containing AMG rules. Numerical experiments demonstrate the potential of these approaches to improve solver performance in large-scale laser beam welding simulations.
Evolving Algebraic Multigrid Methods Using Grammar-Guided Genetic Programming
Dec 08, 2024



Abstract:Multigrid methods despite being known to be asymptotically optimal algorithms, depend on the careful selection of their individual components for efficiency. Also, they are mostly restricted to standard cycle types like V-, F-, and W-cycles. We use grammar rules to generate arbitrary-shaped cycles, wherein the smoothers and their relaxation weights are chosen independently at each step within the cycle. We call this a flexible multigrid cycle. These flexible cycles are used in Algebraic Multigrid (AMG) methods with the help of grammar rules and optimized using genetic programming. The flexible AMG methods are implemented in the software library of hypre, and the programs are optimized separately for two cases: a standalone AMG solver for a 3D anisotropic problem and an AMG preconditioner with conjugate gradient for a multiphysics code. We observe that the optimized flexible cycles provide higher efficiency and better performance than the standard cycle types.
AI Driven Near Real-time Locational Marginal Pricing Method: A Feasibility and Robustness Study
Jun 16, 2023



Abstract:Accurate price predictions are essential for market participants in order to optimize their operational schedules and bidding strategies, especially in the current context where electricity prices become more volatile and less predictable using classical approaches. Locational Marginal Pricing (LMP) pricing mechanism is used in many modern power markets, where the traditional approach utilizes optimal power flow (OPF) solvers. However, for large electricity grids this process becomes prohibitively time-consuming and computationally intensive. Machine learning solutions could provide an efficient tool for LMP prediction, especially in energy markets with intermittent sources like renewable energy. The study evaluates the performance of popular machine learning and deep learning models in predicting LMP on multiple electricity grids. The accuracy and robustness of these models in predicting LMP is assessed considering multiple scenarios. The results show that machine learning models can predict LMP 4-5 orders of magnitude faster than traditional OPF solvers with 5-6\% error rate, highlighting the potential of machine learning models in LMP prediction for large-scale power models with the help of hardware solutions like multi-core CPUs and GPUs in modern HPC clusters.
Evolving Generalizable Multigrid-Based Helmholtz Preconditioners with Grammar-Guided Genetic Programming
Apr 28, 2022

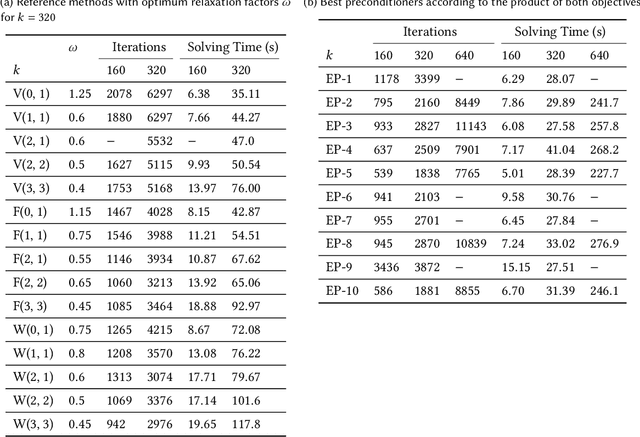

Abstract:Solving the indefinite Helmholtz equation is not only crucial for the understanding of many physical phenomena but also represents an outstandingly-difficult benchmark problem for the successful application of numerical methods. Here we introduce a new approach for evolving efficient preconditioned iterative solvers for Helmholtz problems with multi-objective grammar-guided genetic programming. Our approach is based on a novel context-free grammar, which enables the construction of multigrid preconditioners that employ a tailored sequence of operations on each discretization level. To find solvers that generalize well over the given domain, we propose a custom method of successive problem difficulty adaption, in which we evaluate a preconditioner's efficiency on increasingly ill-conditioned problem instances. We demonstrate our approach's effectiveness by evolving multigrid-based preconditioners for a two-dimensional indefinite Helmholtz problem that outperform several human-designed methods for different wavenumbers up to systems of linear equations with more than a million unknowns.
Known Operator Learning and Hybrid Machine Learning in Medical Imaging --- A Review of the Past, the Present, and the Future
Aug 10, 2021



Abstract:In this article, we perform a review of the state-of-the-art of hybrid machine learning in medical imaging. We start with a short summary of the general developments of the past in machine learning and how general and specialized approaches have been in competition in the past decades. A particular focus will be the theoretical and experimental evidence pro and contra hybrid modelling. Next, we inspect several new developments regarding hybrid machine learning with a particular focus on so-called known operator learning and how hybrid approaches gain more and more momentum across essentially all applications in medical imaging and medical image analysis. As we will point out by numerous examples, hybrid models are taking over in image reconstruction and analysis. Even domains such as physical simulation and scanner and acquisition design are being addressed using machine learning grey box modelling approaches. Towards the end of the article, we will investigate a few future directions and point out relevant areas in which hybrid modelling, meta learning, and other domains will likely be able to drive the state-of-the-art ahead.
Optimizing Geometric Multigrid Methods with Evolutionary Computation
Oct 08, 2019

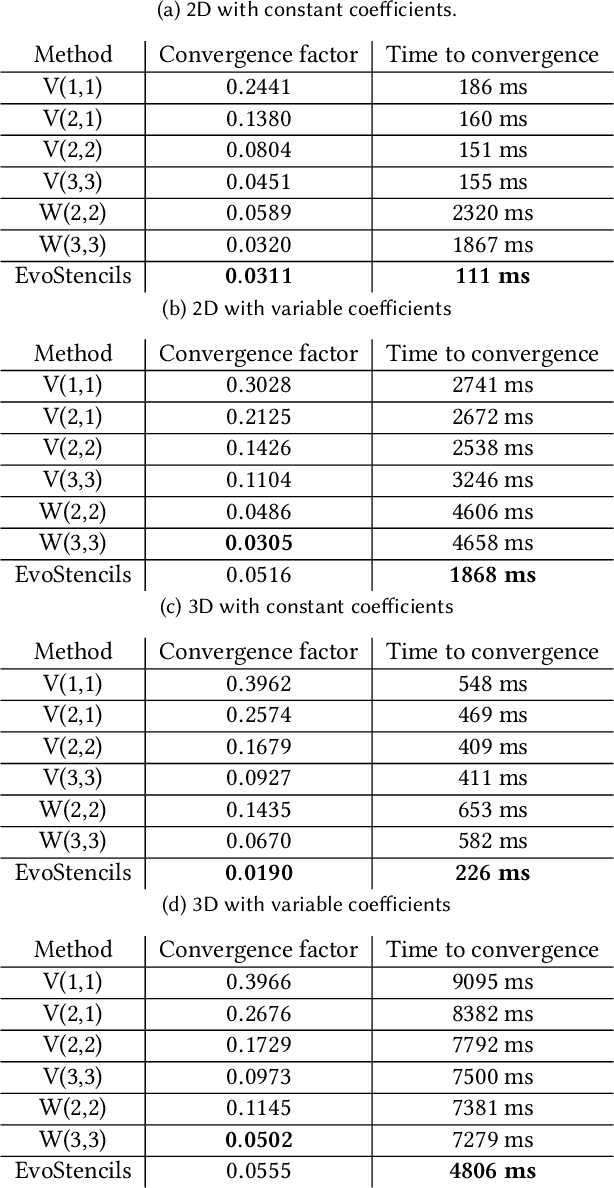
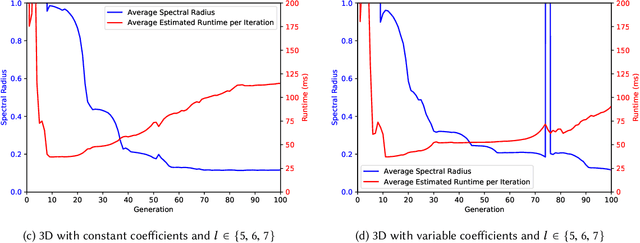
Abstract:For many linear and nonlinear systems that arise from the discretization of partial differential equations the construction of an efficient multigrid solver is a challenging task. Here we present a novel approach for the optimization of geometric multigrid methods that is based on evolutionary computation, a generic program optimization technique inspired by the principle of natural evolution. A multigrid solver is represented as a tree of mathematical expressions which we generate based on a tailored grammar. The quality of each solver is evaluated in terms of convergence and compute performance using automated local Fourier analysis (LFA) and roofline performance modeling, respectively. Based on these objectives a multi-objective optimization is performed using strongly typed genetic programming with a non-dominated sorting based selection. To evaluate the model-based prediction and to target concrete applications, scalable implementations of an evolved solver can be automatically generated with the ExaStencils framework. We demonstrate our approach by constructing multigrid solvers for the steady-state heat equation with constant and variable coefficients that consistently perform better than common V- and W-cycles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge