Comb, Prune, Distill: Towards Unified Pruning for Vision Model Compression

Lightweight and effective models are essential for devices with limited resources, such as intelligent vehicles. Structured pruning offers a promising approach to model compression and efficiency enhancement. However, existing methods often tie pruning techniques to specific model architectures or vision tasks. To address this limitation, we propose a novel unified pruning framework Comb, Prune, Distill (CPD), which addresses both model-agnostic and task-agnostic concerns simultaneously. Our framework employs a combing step to resolve hierarchical layer-wise dependency issues, enabling architecture independence. Additionally, the pruning pipeline adaptively remove parameters based on the importance scoring metrics regardless of vision tasks. To support the model in retaining its learned information, we introduce knowledge distillation during the pruning step. Extensive experiments demonstrate the generalizability of our framework, encompassing both convolutional neural network (CNN) and transformer models, as well as image classification and segmentation tasks. In image classification we achieve a speedup of up to x4.3 with a accuracy loss of 1.8% and in semantic segmentation up to x1.89 with a 5.1% loss in mIoU.

Automating the Design of Multigrid Methods with Evolutionary Program Synthesis

Many of the most fundamental laws of nature can be formulated as partial differential equations (PDEs). Understanding these equations is, therefore, of exceptional importance for many branches of modern science and engineering. However, since the general solution of many PDEs is unknown, the efficient approximate solution of these equations is one of humanity's greatest challenges. While multigrid represents one of the most effective methods for solving PDEs numerically, in many cases, the design of an efficient or at least working multigrid solver is an open problem. This thesis demonstrates that grammar-guided genetic programming, an evolutionary program synthesis technique, can discover multigrid methods of unprecedented structure that achieve a high degree of efficiency and generalization. For this purpose, we develop a novel context-free grammar that enables the automated generation of multigrid methods in a symbolically-manipulable formal language, based on which we can apply the same multigrid-based solver to problems of different sizes without having to adapt its internal structure. Treating the automated design of an efficient multigrid method as a program synthesis task allows us to find novel sequences of multigrid operations, including the combination of different smoothing and coarse-grid correction steps on each level of the discretization hierarchy. To prove the feasibility of this approach, we present its implementation in the form of the Python framework EvoStencils, which is freely available as open-source software. This implementation comprises all steps from representing the algorithmic sequence of a multigrid method in the form of a directed acyclic graph of Python objects to its automatic generation and optimization using the capabilities of the code generation framework ExaStencils and the evolutionary computation library DEAP.

Evolving Generalizable Multigrid-Based Helmholtz Preconditioners with Grammar-Guided Genetic Programming

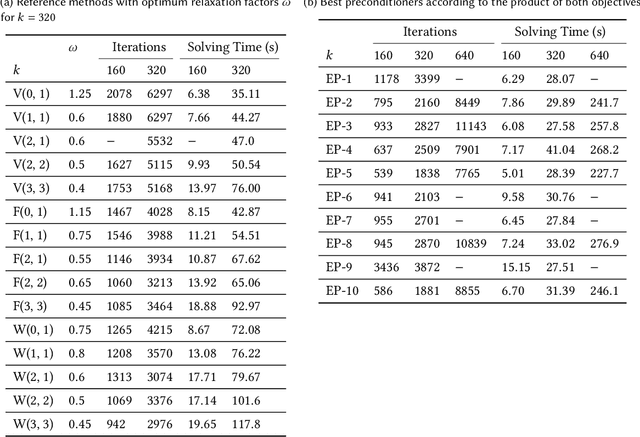
Solving the indefinite Helmholtz equation is not only crucial for the understanding of many physical phenomena but also represents an outstandingly-difficult benchmark problem for the successful application of numerical methods. Here we introduce a new approach for evolving efficient preconditioned iterative solvers for Helmholtz problems with multi-objective grammar-guided genetic programming. Our approach is based on a novel context-free grammar, which enables the construction of multigrid preconditioners that employ a tailored sequence of operations on each discretization level. To find solvers that generalize well over the given domain, we propose a custom method of successive problem difficulty adaption, in which we evaluate a preconditioner's efficiency on increasingly ill-conditioned problem instances. We demonstrate our approach's effectiveness by evolving multigrid-based preconditioners for a two-dimensional indefinite Helmholtz problem that outperform several human-designed methods for different wavenumbers up to systems of linear equations with more than a million unknowns.

Optimizing Geometric Multigrid Methods with Evolutionary Computation

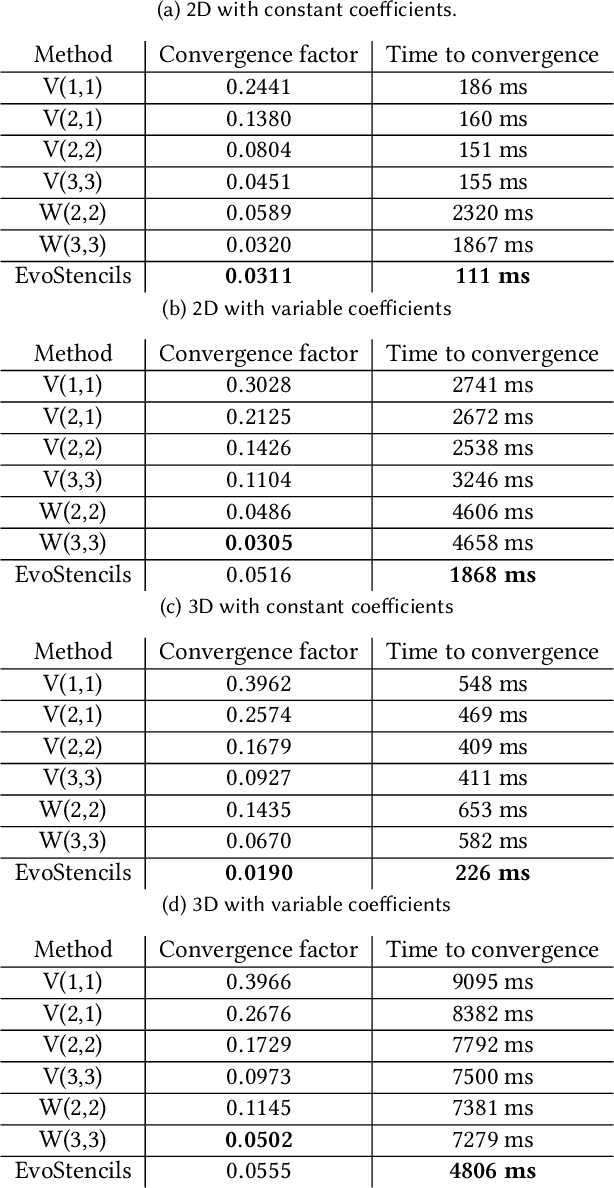
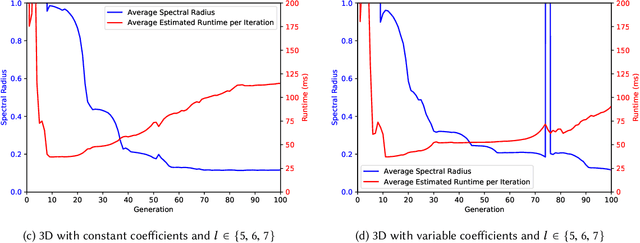
For many linear and nonlinear systems that arise from the discretization of partial differential equations the construction of an efficient multigrid solver is a challenging task. Here we present a novel approach for the optimization of geometric multigrid methods that is based on evolutionary computation, a generic program optimization technique inspired by the principle of natural evolution. A multigrid solver is represented as a tree of mathematical expressions which we generate based on a tailored grammar. The quality of each solver is evaluated in terms of convergence and compute performance using automated local Fourier analysis (LFA) and roofline performance modeling, respectively. Based on these objectives a multi-objective optimization is performed using strongly typed genetic programming with a non-dominated sorting based selection. To evaluate the model-based prediction and to target concrete applications, scalable implementations of an evolved solver can be automatically generated with the ExaStencils framework. We demonstrate our approach by constructing multigrid solvers for the steady-state heat equation with constant and variable coefficients that consistently perform better than common V- and W-cycles.