Evolving Generalizable Multigrid-Based Helmholtz Preconditioners with Grammar-Guided Genetic Programming
Paper and Code
Apr 28, 2022

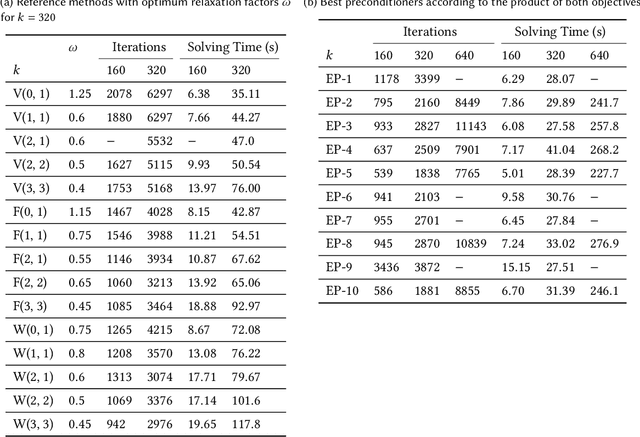

Solving the indefinite Helmholtz equation is not only crucial for the understanding of many physical phenomena but also represents an outstandingly-difficult benchmark problem for the successful application of numerical methods. Here we introduce a new approach for evolving efficient preconditioned iterative solvers for Helmholtz problems with multi-objective grammar-guided genetic programming. Our approach is based on a novel context-free grammar, which enables the construction of multigrid preconditioners that employ a tailored sequence of operations on each discretization level. To find solvers that generalize well over the given domain, we propose a custom method of successive problem difficulty adaption, in which we evaluate a preconditioner's efficiency on increasingly ill-conditioned problem instances. We demonstrate our approach's effectiveness by evolving multigrid-based preconditioners for a two-dimensional indefinite Helmholtz problem that outperform several human-designed methods for different wavenumbers up to systems of linear equations with more than a million unknowns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge