Efficient structure learning with automatic sparsity selection for causal graph processes

We propose a novel algorithm for efficiently computing a sparse directed adjacency matrix from a group of time series following a causal graph process. Our solution is scalable for both dense and sparse graphs and automatically selects the LASSO coefficient to obtain an appropriate number of edges in the adjacency matrix. Current state-of-the-art approaches rely on sparse-matrix-computation libraries to scale, and either avoid automatic selection of the LASSO penalty coefficient or rely on the prediction mean squared error, which is not directly related to the correct number of edges. Instead, we propose a cyclical coordinate descent algorithm that employs two new non-parametric error metrics to automatically select the LASSO coefficient. We demonstrate state-of-the-art performance of our algorithm on simulated stochastic block models and a real dataset of stocks from the S\&P$500$.

Probabilistic Linear Multistep Methods

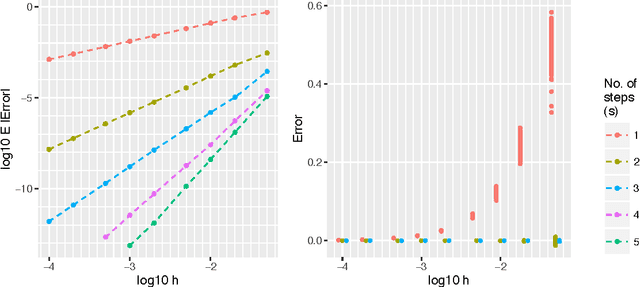
We present a derivation and theoretical investigation of the Adams-Bashforth and Adams-Moulton family of linear multistep methods for solving ordinary differential equations, starting from a Gaussian process (GP) framework. In the limit, this formulation coincides with the classical deterministic methods, which have been used as higher-order initial value problem solvers for over a century. Furthermore, the natural probabilistic framework provided by the GP formulation allows us to derive probabilistic versions of these methods, in the spirit of a number of other probabilistic ODE solvers presented in the recent literature. In contrast to higher-order Runge-Kutta methods, which require multiple intermediate function evaluations per step, Adams family methods make use of previous function evaluations, so that increased accuracy arising from a higher-order multistep approach comes at very little additional computational cost. We show that through a careful choice of covariance function for the GP, the posterior mean and standard deviation over the numerical solution can be made to exactly coincide with the value given by the deterministic method and its local truncation error respectively. We provide a rigorous proof of the convergence of these new methods, as well as an empirical investigation (up to fifth order) demonstrating their convergence rates in practice.