QuACK: A Multipurpose Queuing Algorithm for Cooperative $k$-Armed Bandits

We study the cooperative stochastic $k$-armed bandit problem, where a network of $m$ agents collaborate to find the optimal action. In contrast to most prior work on this problem, which focuses on extending a specific algorithm to the multi-agent setting, we provide a black-box reduction that allows us to extend any single-agent bandit algorithm to the multi-agent setting. Under mild assumptions on the bandit environment, we prove that our reduction transfers the regret guarantees of the single-agent algorithm to the multi-agent setting. These guarantees are tight in subgaussian environments, in that using a near minimax optimal single-player algorithm is near minimax optimal in the multi-player setting up to an additive graph-dependent quantity. Our reduction and theoretical results are also general, and apply to many different bandit settings. By plugging in appropriate single-player algorithms, we can easily develop provably efficient algorithms for many multi-player settings such as heavy-tailed bandits, duelling bandits and bandits with local differential privacy, among others. Experimentally, our approach is competitive with or outperforms specialised multi-agent algorithms.

"How Big is Big Enough?" Adjusting Model Size in Continual Gaussian Processes

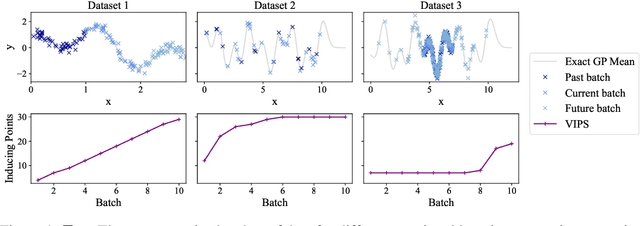
For many machine learning methods, creating a model requires setting a parameter that controls the model's capacity before training, e.g.~number of neurons in DNNs, or inducing points in GPs. Increasing capacity improves performance until all the information from the dataset is captured. After this point, computational cost keeps increasing, without improved performance. This leads to the question ``How big is big enough?'' We investigate this problem for Gaussian processes (single-layer neural networks) in continual learning. Here, data becomes available incrementally, and the final dataset size will therefore not be known before training, preventing the use of heuristics for setting the model size. We provide a method that automatically adjusts this, while maintaining near-optimal performance, and show that a single hyperparameter setting for our method performs well across datasets with a wide range of properties.

Logistic Variational Bayes Revisited

Variational logistic regression is a popular method for approximate Bayesian inference seeing wide-spread use in many areas of machine learning including: Bayesian optimization, reinforcement learning and multi-instance learning to name a few. However, due to the intractability of the Evidence Lower Bound, authors have turned to the use of Monte Carlo, quadrature or bounds to perform inference, methods which are costly or give poor approximations to the true posterior. In this paper we introduce a new bound for the expectation of softplus function and subsequently show how this can be applied to variational logistic regression and Gaussian process classification. Unlike other bounds, our proposal does not rely on extending the variational family, or introducing additional parameters to ensure the bound is tight. In fact, we show that this bound is tighter than the state-of-the-art, and that the resulting variational posterior achieves state-of-the-art performance, whilst being significantly faster to compute than Monte-Carlo methods.

Mixed-Output Gaussian Process Latent Variable Models

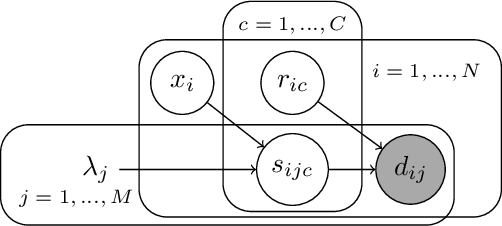
This work develops a Bayesian non-parametric approach to signal separation where the signals may vary according to latent variables. Our key contribution is to augment Gaussian Process Latent Variable Models (GPLVMs) to incorporate the case where each data point comprises the weighted sum of a known number of pure component signals, observed across several input locations. Our framework allows the use of a range of priors for the weights of each observation. This flexibility enables us to represent use cases including sum-to-one constraints for estimating fractional makeup, and binary weights for classification. Our contributions are particularly relevant to spectroscopy, where changing conditions may cause the underlying pure component signals to vary from sample to sample. To demonstrate the applicability to both spectroscopy and other domains, we consider several applications: a near-infrared spectroscopy data set with varying temperatures, a simulated data set for identifying flow configuration through a pipe, and a data set for determining the type of rock from its reflectance.

Delayed Feedback in Generalised Linear Bandits Revisited

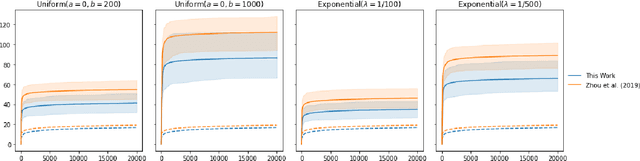
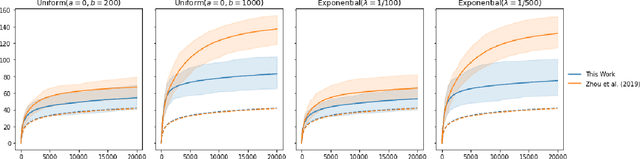
The stochastic generalised linear bandit is a well-understood model for sequential decision-making problems, with many algorithms achieving near-optimal regret guarantees under immediate feedback. However, in many real world settings, the requirement that the reward is observed immediately is not applicable. In this setting, standard algorithms are no longer theoretically understood. We study the phenomenon of delayed rewards in a theoretical manner by introducing a delay between selecting an action and receiving the reward. Subsequently, we show that an algorithm based on the optimistic principle improves on existing approaches for this setting by eliminating the need for prior knowledge of the delay distribution and relaxing assumptions on the decision set and the delays. This also leads to improving the regret guarantees from $ \widetilde O(\sqrt{dT}\sqrt{d + \mathbb{E}[\tau]})$ to $ \widetilde O(d\sqrt{T} + d^{3/2}\mathbb{E}[\tau])$, where $\mathbb{E}[\tau]$ denotes the expected delay, $d$ is the dimension and $T$ the time horizon and we have suppressed logarithmic terms. We verify our theoretical results through experiments on simulated data.

Variational Bayes for high-dimensional proportional hazards models with applications to gene expression variable selection

We propose a variational Bayesian proportional hazards model for prediction and variable selection regarding high-dimensional survival data. Our method, based on a mean-field variational approximation, overcomes the high computational cost of MCMC whilst retaining the useful features, providing excellent point estimates and offering a natural mechanism for variable selection via posterior inclusion probabilities. The performance of our proposed method is assessed via extensive simulations and compared against other state-of-the-art Bayesian variable selection methods, demonstrating comparable or better performance. Finally, we demonstrate how the proposed method can be used for variable selection on two transcriptomic datasets with censored survival outcomes, where we identify genes with pre-existing biological interpretations.

Delayed Feedback in Episodic Reinforcement Learning

There are many provably efficient algorithms for episodic reinforcement learning. However, these algorithms are built under the assumption that the sequences of states, actions and rewards associated with each episode arrive immediately, allowing policy updates after every interaction with the environment. This assumption is often unrealistic in practice, particularly in areas such as healthcare and online recommendation. In this paper, we study the impact of delayed feedback on several provably efficient algorithms for regret minimisation in episodic reinforcement learning. Firstly, we consider updating the policy as soon as new feedback becomes available. Using this updating scheme, we show that the regret increases by an additive term involving the number of states, actions, episode length and the expected delay. This additive term changes depending on the optimistic algorithm of choice. We also show that updating the policy less frequently can lead to an improved dependency of the regret on the delays.

BART-based inference for Poisson processes

The effectiveness of Bayesian Additive Regression Trees (BART) has been demonstrated in a variety of contexts including non parametric regression and classification. Here we introduce a BART scheme for estimating the intensity of inhomogeneous Poisson Processes. Poisson intensity estimation is a vital task in various applications including medical imaging, astrophysics and network traffic analysis. Our approach enables full posterior inference of the intensity in a nonparametric regression setting. We demonstrate the performance of our scheme through simulation studies on synthetic and real datasets in one and two dimensions, and compare our approach to alternative approaches.

A Bayesian nonparametric test for conditional independence

This article introduces a Bayesian nonparametric method for quantifying the relative evidence in a dataset in favour of the dependence or independence of two variables conditional on a third. The approach uses Polya tree priors on spaces of conditional probability densities, accounting for uncertainty in the form of the underlying distributions in a nonparametric way. The Bayesian perspective provides an inherently symmetric probability measure of conditional dependence or independence, a feature particularly advantageous in causal discovery and not employed by any previous procedure of this type.

Interpreting Deep Neural Networks Through Variable Importance

While the success of deep neural networks (DNNs) is well-established across a variety of domains, our ability to explain and interpret these methods is limited. Unlike previously proposed local methods which try to explain particular classification decisions, we focus on global interpretability and ask a universally applicable question: given a trained model, which features are the most important? In the context of neural networks, a feature is rarely important on its own, so our strategy is specifically designed to leverage partial covariance structures and incorporate variable dependence into feature ranking. Our methodological contributions in this paper are two-fold. First, we propose an effect size analogue for DNNs that is appropriate for applications with highly collinear predictors (ubiquitous in computer vision). Second, we extend the recently proposed "RelATive cEntrality" (RATE) measure (Crawford et al., 2019) to the Bayesian deep learning setting. RATE applies an information theoretic criterion to the posterior distribution of effect sizes to assess feature significance. We apply our framework to three broad application areas: computer vision, natural language processing, and social science.