QuACK: A Multipurpose Queuing Algorithm for Cooperative $k$-Armed Bandits

We study the cooperative stochastic $k$-armed bandit problem, where a network of $m$ agents collaborate to find the optimal action. In contrast to most prior work on this problem, which focuses on extending a specific algorithm to the multi-agent setting, we provide a black-box reduction that allows us to extend any single-agent bandit algorithm to the multi-agent setting. Under mild assumptions on the bandit environment, we prove that our reduction transfers the regret guarantees of the single-agent algorithm to the multi-agent setting. These guarantees are tight in subgaussian environments, in that using a near minimax optimal single-player algorithm is near minimax optimal in the multi-player setting up to an additive graph-dependent quantity. Our reduction and theoretical results are also general, and apply to many different bandit settings. By plugging in appropriate single-player algorithms, we can easily develop provably efficient algorithms for many multi-player settings such as heavy-tailed bandits, duelling bandits and bandits with local differential privacy, among others. Experimentally, our approach is competitive with or outperforms specialised multi-agent algorithms.

DISCO: An End-to-End Bandit Framework for Personalised Discount Allocation

Personalised discount codes provide a powerful mechanism for managing customer relationships and operational spend in e-commerce. Bandits are well suited for this product area, given the partial information nature of the problem, as well as the need for adaptation to the changing business environment. Here, we introduce DISCO, an end-to-end contextual bandit framework for personalised discount code allocation at ASOS. DISCO adapts the traditional Thompson Sampling algorithm by integrating it within an integer program, thereby allowing for operational cost control. Because bandit learning is often worse with high dimensional actions, we focused on building low dimensional action and context representations that were nonetheless capable of good accuracy. Additionally, we sought to build a model that preserved the relationship between price and sales, in which customers increasing their purchasing in response to lower prices ("negative price elasticity"). These aims were achieved by using radial basis functions to represent the continuous (i.e. infinite armed) action space, in combination with context embeddings extracted from a neural network. These feature representations were used within a Thompson Sampling framework to facilitate exploration, and further integrated with an integer program to allocate discount codes across ASOS's customer base. These modelling decisions result in a reward model that (a) enables pooled learning across similar actions, (b) is highly accurate, including in extrapolation, and (c) preserves the expected negative price elasticity. Through offline analysis, we show that DISCO is able to effectively enact exploration and improves its performance over time, despite the global constraint. Finally, we subjected DISCO to a rigorous online A/B test, and find that it achieves a significant improvement of >1% in average basket value, relative to the legacy systems.

Delayed Feedback in Generalised Linear Bandits Revisited

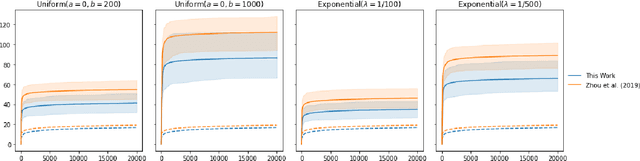
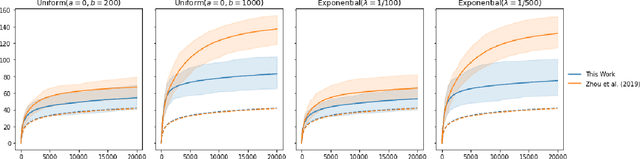
The stochastic generalised linear bandit is a well-understood model for sequential decision-making problems, with many algorithms achieving near-optimal regret guarantees under immediate feedback. However, in many real world settings, the requirement that the reward is observed immediately is not applicable. In this setting, standard algorithms are no longer theoretically understood. We study the phenomenon of delayed rewards in a theoretical manner by introducing a delay between selecting an action and receiving the reward. Subsequently, we show that an algorithm based on the optimistic principle improves on existing approaches for this setting by eliminating the need for prior knowledge of the delay distribution and relaxing assumptions on the decision set and the delays. This also leads to improving the regret guarantees from $ \widetilde O(\sqrt{dT}\sqrt{d + \mathbb{E}[\tau]})$ to $ \widetilde O(d\sqrt{T} + d^{3/2}\mathbb{E}[\tau])$, where $\mathbb{E}[\tau]$ denotes the expected delay, $d$ is the dimension and $T$ the time horizon and we have suppressed logarithmic terms. We verify our theoretical results through experiments on simulated data.

Delayed Feedback in Episodic Reinforcement Learning

There are many provably efficient algorithms for episodic reinforcement learning. However, these algorithms are built under the assumption that the sequences of states, actions and rewards associated with each episode arrive immediately, allowing policy updates after every interaction with the environment. This assumption is often unrealistic in practice, particularly in areas such as healthcare and online recommendation. In this paper, we study the impact of delayed feedback on several provably efficient algorithms for regret minimisation in episodic reinforcement learning. Firstly, we consider updating the policy as soon as new feedback becomes available. Using this updating scheme, we show that the regret increases by an additive term involving the number of states, actions, episode length and the expected delay. This additive term changes depending on the optimistic algorithm of choice. We also show that updating the policy less frequently can lead to an improved dependency of the regret on the delays.