Correlating Variational Autoencoders Natively For Multi-View Imputation

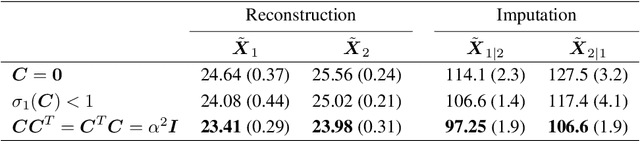
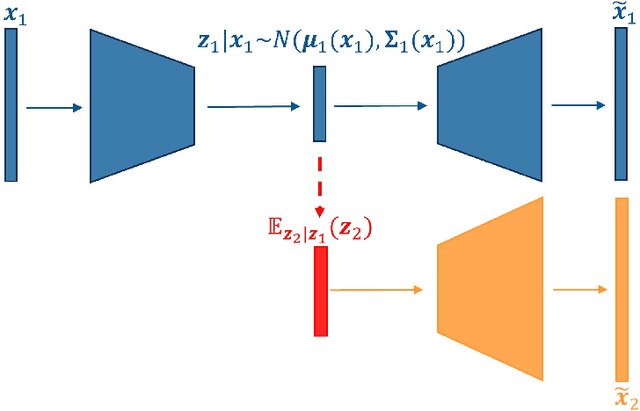
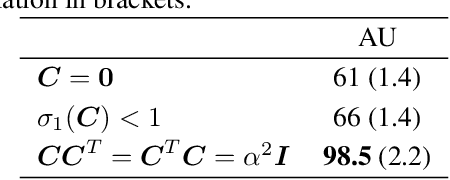
Multi-view data from the same source often exhibit correlation. This is mirrored in correlation between the latent spaces of separate variational autoencoders (VAEs) trained on each data-view. A multi-view VAE approach is proposed that incorporates a joint prior with a non-zero correlation structure between the latent spaces of the VAEs. By enforcing such correlation structure, more strongly correlated latent spaces are uncovered. Using conditional distributions to move between these latent spaces, missing views can be imputed and used for downstream analysis. Learning this correlation structure involves maintaining validity of the prior distribution, as well as a successful parameterization that allows end-to-end learning.

Logistic Variational Bayes Revisited

Variational logistic regression is a popular method for approximate Bayesian inference seeing wide-spread use in many areas of machine learning including: Bayesian optimization, reinforcement learning and multi-instance learning to name a few. However, due to the intractability of the Evidence Lower Bound, authors have turned to the use of Monte Carlo, quadrature or bounds to perform inference, methods which are costly or give poor approximations to the true posterior. In this paper we introduce a new bound for the expectation of softplus function and subsequently show how this can be applied to variational logistic regression and Gaussian process classification. Unlike other bounds, our proposal does not rely on extending the variational family, or introducing additional parameters to ensure the bound is tight. In fact, we show that this bound is tighter than the state-of-the-art, and that the resulting variational posterior achieves state-of-the-art performance, whilst being significantly faster to compute than Monte-Carlo methods.

Dual feature reduction for the sparse-group lasso and its adaptive variant

The sparse-group lasso performs both variable and group selection, making simultaneous use of the strengths of the lasso and group lasso. It has found widespread use in genetics, a field that regularly involves the analysis of high-dimensional data, due to its sparse-group penalty, which allows it to utilize grouping information. However, the sparse-group lasso can be computationally more expensive than both the lasso and group lasso, due to the added shrinkage complexity, and its additional hyper-parameter that needs tuning. In this paper a novel dual feature reduction method, Dual Feature Reduction (DFR), is presented that uses strong screening rules for the sparse-group lasso and the adaptive sparse-group lasso to reduce their input space before optimization. DFR applies two layers of screening and is based on the dual norms of the sparse-group lasso and adaptive sparse-group lasso. Through synthetic and real numerical studies, it is shown that the proposed feature reduction approach is able to drastically reduce the computational cost in many different scenarios.

Strong screening rules for group-based SLOPE models

Tuning the regularization parameter in penalized regression models is an expensive task, requiring multiple models to be fit along a path of parameters. Strong screening rules drastically reduce computational costs by lowering the dimensionality of the input prior to fitting. We develop strong screening rules for group-based Sorted L-One Penalized Estimation (SLOPE) models: Group SLOPE and Sparse-group SLOPE. The developed rules are applicable for the wider family of group-based OWL models, including OSCAR. Our experiments on both synthetic and real data show that the screening rules significantly accelerate the fitting process. The screening rules make it accessible for group SLOPE and sparse-group SLOPE to be applied to high-dimensional datasets, particularly those encountered in genetics.

Variational Bayes for high-dimensional proportional hazards models with applications to gene expression variable selection

We propose a variational Bayesian proportional hazards model for prediction and variable selection regarding high-dimensional survival data. Our method, based on a mean-field variational approximation, overcomes the high computational cost of MCMC whilst retaining the useful features, providing excellent point estimates and offering a natural mechanism for variable selection via posterior inclusion probabilities. The performance of our proposed method is assessed via extensive simulations and compared against other state-of-the-art Bayesian variable selection methods, demonstrating comparable or better performance. Finally, we demonstrate how the proposed method can be used for variable selection on two transcriptomic datasets with censored survival outcomes, where we identify genes with pre-existing biological interpretations.

S-multi-SNE: Semi-Supervised Classification and Visualisation of Multi-View Data

An increasing number of multi-view data are being published by studies in several fields. This type of data corresponds to multiple data-views, each representing a different aspect of the same set of samples. We have recently proposed multi-SNE, an extension of t-SNE, that produces a single visualisation of multi-view data. The multi-SNE approach provides low-dimensional embeddings of the samples, produced by being updated iteratively through the different data-views. Here, we further extend multi-SNE to a semi-supervised approach, that classifies unlabelled samples by regarding the labelling information as an extra data-view. We look deeper into the performance, limitations and strengths of multi-SNE and its extension, S-multi-SNE, by applying the two methods on various multi-view datasets with different challenges. We show that by including the labelling information, the projection of the samples improves drastically and it is accompanied by a strong classification performance.

Multi-view Data Visualisation via Manifold Learning

Manifold learning approaches, such as Stochastic Neighbour Embedding (SNE), Locally Linear Embedding (LLE) and Isometric Feature Mapping (ISOMAP) have been proposed for performing non-linear dimensionality reduction. These methods aim to produce two or three latent embeddings, in order to visualise the data in intelligible representations. This manuscript proposes extensions of Student's t-distributed SNE (t-SNE), LLE and ISOMAP, to allow for dimensionality reduction and subsequent visualisation of multi-view data. Nowadays, it is very common to have multiple data-views on the same samples. Each data-view contains a set of features describing different aspects of the samples. For example, in biomedical studies it is possible to generate multiple OMICS data sets for the same individuals, such as transcriptomics, genomics, epigenomics, enabling better understanding of the relationships between the different biological processes. Through the analysis of real and simulated datasets, the visualisation performance of the proposed methods is illustrated. Data visualisations have been often utilised for identifying any potential clusters in the data sets. We show that by incorporating the low-dimensional embeddings obtained via the multi-view manifold learning approaches into the K-means algorithm, clusters of the samples are accurately identified. Our proposed multi-SNE method outperforms the corresponding multi-ISOMAP and multi-LLE proposed methods. Interestingly, multi-SNE is found to have comparable performance with methods proposed in the literature for performing multi-view clustering.